
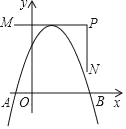
【题目】如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则a﹣b+c的最小值是_____.
科目:初中数学 来源: 题型:
【题目】我们知道:sin30°=![]() ,tan30°=
,tan30°=![]() ,sin45°=
,sin45°=![]() ,tan45°=1,sin60°=
,tan45°=1,sin60°=![]() ,tan60°=
,tan60°=![]() ,由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
,由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=120°,点A,B分別在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°,且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD.
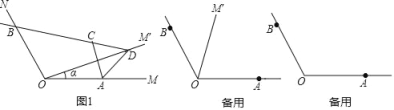
(1)求证:AD=CD;
(2)如图1,当0°<α<60°时,试证明∠ACD的大小是一个定值;
(3)当60°<α<120°时,(2)中的结论还成立吗?请补全图形并说明理由;
(4)△ACD面积的最大值为 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
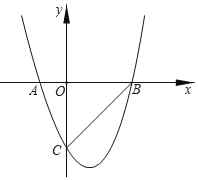
【题目】如图,二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,则下列说法错误的是( )
A. AB=4
B. ∠ABC=45°
C. 当x>0时,y<﹣3
D. 当x>1时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在利用描点法画二次函数y=ax2+bx+c(a=0)的图象时,先取自变量x的一些值,计算出相应的函数值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | ﹣3 | … |
接着,他在描点时发现,表格中有一组数据计算错误,他计算错误的一组数据是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
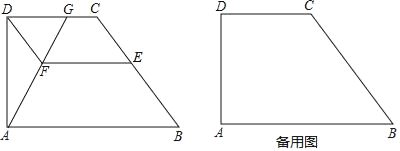
【题目】如图,已知梯形ABCD中,AB∥CD,∠DAB=90°,AD=4,AB=2CD=6,E是边BC上一点,过点D、E分别作BC、CD的平行线交于点F,联结AF并延长,与射线DC交于点G.
(1)当点G与点C重合时,求CE:BE的值;
(2)当点G在边CD上时,设CE=m,求△DFG的面积;(用含m的代数式表示)
(3)当△AFD∽△ADG时,求∠DAG的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
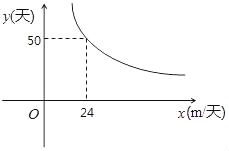
【题目】在工程实施过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成工程量x米的函数关系图象如图所示,是双曲线的一部分.
(1)请根据题意,求y与x之间的函数表达式;
(2)若该工程队有2台挖掘机,每台挖掘机每天能够开挖水渠30米,问该工程队需要用多少天才能完成此项任务?
(3)如果为了防汛工作的紧急需要,必须在10天内完成任务,那么每天至少要完成多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com