
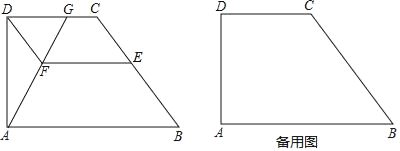
【题目】如图,已知梯形ABCD中,AB∥CD,∠DAB=90°,AD=4,AB=2CD=6,E是边BC上一点,过点D、E分别作BC、CD的平行线交于点F,联结AF并延长,与射线DC交于点G.
(1)当点G与点C重合时,求CE:BE的值;
(2)当点G在边CD上时,设CE=m,求△DFG的面积;(用含m的代数式表示)
(3)当△AFD∽△ADG时,求∠DAG的余弦值.
【答案】(1)EC:BE=1:1;(2)S△DFG=![]() ;(3)cos∠DAG=
;(3)cos∠DAG=![]() .
.
【解析】
(1)由题意可得四边形DCEF是平行四边形,可得CD=EF,通过证明△CFE∽△CAB,可得![]() ,从而BE=CE,则可求CE:BE的值;
,从而BE=CE,则可求CE:BE的值;
(2)延长AG,BC交为于点M,过点C作CN⊥AB于点N,交EF于点H,由题意可得四边形ADCN是矩形,可得AD=CN=4,CD=AN=3,BN=3,由平行线分线段成比例可求BE,ME,MC,CH,GC的长,即可求GD的长,由三角求形面积公式可△DFG的面积;
(3)由△AFD∽△ADG,可得∠AFD=∠ADG=90°,由余角的性质可得∠DAG=∠B,即可求∠DAG的余弦值.
(1)如图,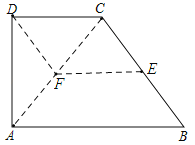
∵DC∥EF,DF∥CE,∴四边形DCEF是平行四边形,∴CD=EF.
∵AB=2CD=6,∴AB=2EF.
∵EF∥CD,AB∥CD,∴EF∥AB,∴△CFE∽△CAB,∴![]() ,∴BC=2CE,∴BE=CE,∴EC:BE=1:1.
,∴BC=2CE,∴BE=CE,∴EC:BE=1:1.
(2)如图,延长AG,BC交为于点M,过点C作CN⊥AB于点N,交EF于点H.
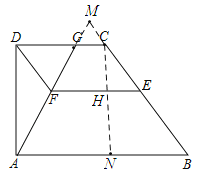
∵AD⊥CD,CN⊥CD,∴AD∥CN,且CD∥AB,∴四边形ADCN是平行四边形.
又∵∠DAB=90°,∴四边形ADCN是矩形,∴AD=CN=4,CD=AN=3,∴BN=AB﹣AN=3.
在Rt△BCN中,BC![]() 5,∴BE=BC﹣CE=5﹣m.
5,∴BE=BC﹣CE=5﹣m.
∵EF∥AB,∴![]() ,即
,即![]() ,∴ME=BE=5﹣m,∴MC=ME﹣CE=5﹣2m.
,∴ME=BE=5﹣m,∴MC=ME﹣CE=5﹣2m.
∵EF∥AB,∴![]() ,∴HC
,∴HC![]() m.
m.
∵CG∥EF,∴![]() ,即
,即![]() ,∴GC
,∴GC![]() ,∴DG=CD﹣GC=3
,∴DG=CD﹣GC=3![]() ,∴S△DFG
,∴S△DFG![]() DG×CH
DG×CH![]() .
.
(3)过点C作CN⊥AB于点N.
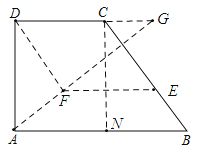
∵AB∥CD,∠DAB=90°,∴∠DAB=∠ADG=90°,若△AFD∽△ADG,∴∠AFD=∠ADG=90°,∴DF⊥AG.
又∵DF∥BC,∴AG⊥BC,∴∠B+∠GAB=90°,且∠DAG+∠GAB=90°,∴∠B=∠DAG,∴cos∠DAG=cosB![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是太阳能电池板支撑架的截面图,其中AB=300cm,AB的倾斜角为30°,BE=CA=50cm,FE⊥AB于点E.点D、F到地面的垂直距离均为30cm,点A到地面的垂直距离为50cm.求CD和EF的长度各是多少cm(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
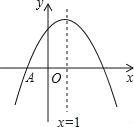
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
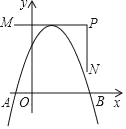
【题目】如图,抛物线y=ax2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则a﹣b+c的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
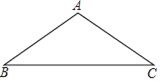
【题目】如图,在△ABC中,AB=AC=5,sinC=![]() ,将△ABC绕点A逆时针旋转得到△ADE,点B、C分别与点D、E对应,AD与边BC交于点F.如果AE∥BC,那么BF的长是____.
,将△ABC绕点A逆时针旋转得到△ADE,点B、C分别与点D、E对应,AD与边BC交于点F.如果AE∥BC,那么BF的长是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
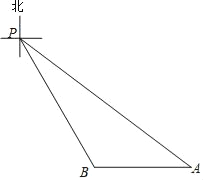
【题目】如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距20![]() 海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)试问船B在灯塔P的什么方向?
(2)求两船相距多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
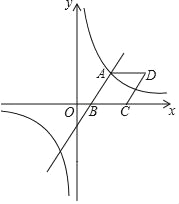
【题目】如图,已知一次函数y=2x﹣4与反比例函数y=![]() 的图象相交于点A(a,2),与x轴相交于点B.
的图象相交于点A(a,2),与x轴相交于点B.
(1)求a和k的值;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求菱形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com