
【题目】如图是太阳能电池板支撑架的截面图,其中AB=300cm,AB的倾斜角为30°,BE=CA=50cm,FE⊥AB于点E.点D、F到地面的垂直距离均为30cm,点A到地面的垂直距离为50cm.求CD和EF的长度各是多少cm(结果保留根号).

【答案】CD和EF的长度分别是45cm和![]() cm.
cm.
【解析】
过A作AG⊥CD于G,连接FD并延长,与BA的延长线交于H,在Rt△CDH和Rt△EFH中通过解直角三角形,即可得到CD和EF的长度.
解:过A作AG⊥CD于G,则∠CAG=30°,
在Rt△ACG中,CG=ACsin30°=50×![]() =25,
=25,
∵GD=50﹣30=20,
∴CD=CG+GD=25+20=45,
连接FD并延长,与BA的延长线交于H,则∠H=30°,
在Rt△CDH中,CH=![]() =2CD=90,
=2CD=90,
∴EH=EC+CH=AB﹣BE﹣AC+CH=300﹣50﹣50+90=290,
在Rt△EFH中,EF=EHtan30°=290×![]() =
=![]() ,
,
答:CD和EF的长度分别是45cm和![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】一个正方形AOBC各顶点的坐标分别为A(0,3),O(0,0),B(3,0),C(3,3).若以原点为位似中心,将这个正方形的边长缩小为原来的![]() ,则新正方形的中心的坐标为_____.
,则新正方形的中心的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
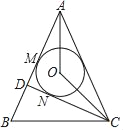
【题目】如图,AB=AC,CD⊥AB于点D,点O是∠BAC的平分线上一点,⊙O与AB相切于点M,与CD相切于点N
(1)求证:∠AOC=135°;
(2)若NC=3,BC=2![]() ,求DM的长.
,求DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:sin30°=![]() ,tan30°=
,tan30°=![]() ,sin45°=
,sin45°=![]() ,tan45°=1,sin60°=
,tan45°=1,sin60°=![]() ,tan60°=
,tan60°=![]() ,由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
,由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
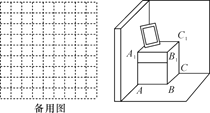
【题目】如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.
(1)请你在备用图中画出蚂蚁能够最快到达目的地的可能路径;
(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
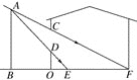
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过原点且与x轴交于点A,顶点的纵坐标是
过原点且与x轴交于点A,顶点的纵坐标是![]() .
.
![]() 求抛物线的函数表达式及点A坐标;
求抛物线的函数表达式及点A坐标;
![]() 根据图象回答:当x为何值时抛物线位于x轴上方?
根据图象回答:当x为何值时抛物线位于x轴上方?
![]() 直接写出所求抛物线先向左平移3个单位,再向上平移5个单位所得到抛物线的函数表达式.
直接写出所求抛物线先向左平移3个单位,再向上平移5个单位所得到抛物线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
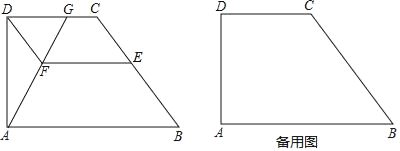
【题目】如图,已知梯形ABCD中,AB∥CD,∠DAB=90°,AD=4,AB=2CD=6,E是边BC上一点,过点D、E分别作BC、CD的平行线交于点F,联结AF并延长,与射线DC交于点G.
(1)当点G与点C重合时,求CE:BE的值;
(2)当点G在边CD上时,设CE=m,求△DFG的面积;(用含m的代数式表示)
(3)当△AFD∽△ADG时,求∠DAG的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com