
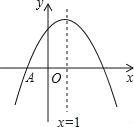
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
利用抛物线的开口方向可得a<0,再由抛物线的对称轴可得b=-2a,由此可对①进行判断;利用2≤c≤3结合已知条件可对②进行判断;利用二次函数的性质可对③进行判断;根据抛物线y=ax2+bx+c直线y=n-1的交点个数可对④进行判断.
∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=![]() =1,
=1,
∴b=-2a,
∴3a+b=3a-2a=a<0,故①正确;
∵抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),
∴a-b+c=0,∴c=-3a,
∵2≤c≤3,
∴2≤-3a≤3,
∴﹣1≤a≤﹣![]() ,故②正确;
,故②正确;
∵抛物线的顶点坐标为(1,n),
∴x=1时,二次函数有最大值为n,
∴对于任意实数m ,总有a+b+c≥am2+bm+c,
即a+b≥am2+bm,故③正确;
∵抛物线的顶点坐标为(1,n),
∴抛物线y=ax2+bx+c直线y=n-1有两个交点,
∴关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根,故④正确,
故选D.


科目:初中数学 来源: 题型:
【题目】我们把三边长的比为3:4:5的三角形称为完全三角形,记命题A:“完全三角形是直角三角形”.若命题B是命题A的逆命题,请写出命题B:______________________;并写出一个例子(该例子能判断命题B是错误的)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图所示是一条线段,AB的长为10厘米,MN的长为2厘米,假设可以随意在这条线段上取一点,求这个点取在线段MN上的概率.
(2)如图是一个木制圆盘,图中两同心圆,其中大圆直径为20cm,小圆的直径为10cm,一只小鸟自由自在地在空中飞行,求小鸟停在小圆内(阴影部分)的概率是 .
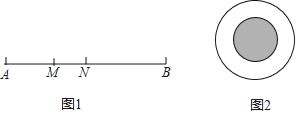
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥周谷堆农副产品批发市场某商铺购进一批红薯,通过商店批发和在淘宝网上进行销售.首月进行了销售情况的统计,其中商店日批发量![]() (百斤)与时间
(百斤)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;在淘宝网上的日销售量
为整数,单位:天)的部分对应值如下表所示;在淘宝网上的日销售量![]() (百斤)与时间
(百斤)与时间![]() (
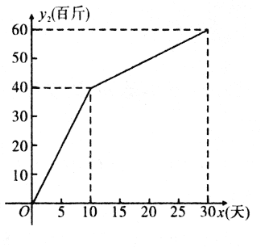
(![]() 为整数,单位:天)的部分对应值如图所示.
为整数,单位:天)的部分对应值如图所示.
时间 | 0 | 5 | 10 | 150 | 20 | 25 | 30 |
日批发量 | 025 | 40 | 45 | 40 | 25 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映![]() 与
与![]() 的变化规律,求出
的变化规律,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)设这个月中,日销售总量为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并求出当
之间的函数关系式,并求出当![]() 为何值时,日销售总量
为何值时,日销售总量![]() 最大,最大值为多少?
最大,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
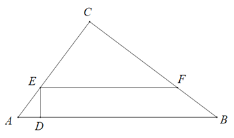
【题目】如图,在直角△ABC中,∠C=90°,AC=15,BC=20,点D为AB边上一动点,若AD的长度为m,且m的范围为0<m<9,在AC与BC边上分别取两点E、F,满足ED⊥AB,FE⊥ED.
(1)求DE的长度;(用含m的代数式表示)
(2)求EF的长度;(用含m的代数式表示)
(3)请根据m的不同取值,探索过D、E、F三点的圆与△ABC三边交点的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有5个分别写有数字﹣2,﹣1,1,2,3的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字作为点P的横坐标,将该数的绝对值作为点P的纵坐标,则点P落在抛物线y=﹣x2+2x+4与x轴所围成的区域内(不含边界)的概率是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com