
����Ŀ����ͼ���ı���ABCD�Ǿ���ֽƬ��AB=2�����۾���ֽƬABCD��ʹAD��BC�غϣ��ۺ�ΪEF��չƽ���ٹ���B�۵�����ֽƬ��ʹ��A����EF�ϵĵ�N���ۺ�BM��EF�ཻ�ڵ�Q���ٴ�չƽ������BN��MN���ӳ�MN��BC�ڵ�G�������½��ۣ�
�١�ABN=60�㣻��AM=1����QN= ![]() ���ܡ�BMG�ǵȱ������Σ���PΪ�߶�BM��һ���㣬H��BN���е㣬��PN+PH����Сֵ��
���ܡ�BMG�ǵȱ������Σ���PΪ�߶�BM��һ���㣬H��BN���е㣬��PN+PH����Сֵ�� ![]() ��
��
������ȷ���۵������ �� 
���𰸡��٢ܢ�
���������⣺��ͼ1������AN��
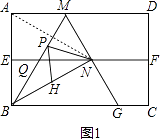
��EF��ֱƽ��AB��
��AN=BN��
�����۵������ʣ��ɵ�
AB=BN��
��AN=AB=BN��
���ABNΪ�ȱ������Σ�
���ABN=60�㣬��PBN=60���2=30�㣬
�����ۢ���ȷ��
�ߡ�ABN=60�㣬��ABM=��NBM��
���ABM=��NBM=60���2=30�㣬
��AM= ![]() ��
��
�����ۢڲ���ȷ��
��EF��BC��QN�ǡ�MBG����λ�ߣ�
��QN= ![]() BG��
BG��
��BG=BM= ![]() ��
��
��QN= ![]() ��
��
�����ۢ۲���ȷ��
�ߡ�ABM=��MBN=30�㣬��BNM=��BAM=90�㣬
���BMG=��BNM����MBN=90�㩁30��=60�㣬
���MBG=��ABG����ABM=90�㩁30��=60�㣬
���BGM=180�㩁60�㩁60��=60�㣬
���MBG=��BMG=��BGM=60�㣬
���BMGΪ�ȱ������Σ�
�����ۢ���ȷ��
�ߡ�BMG�ǵȱ������Σ���N��MG���е㣬
��BN��MG����BN=BGsin60��= ![]() ��
��
����������֪E���H�����BM�Գƣ���PH=PE��
��P��Q�غ�ʱ��PN+PH��ֵ��С����ʱPN+PH=PN+PE=EN��
��EN= ![]() =
= ![]() ��
��
��PN+PH= ![]() ��
��
��PN+PH����Сֵ�� ![]() ��
��
�����ۢ���ȷ��
���Դ��ǣ��٢ܢݣ�
�����㾫�������ڱ��⿼�����Գ�-���·�����⣬��Ҫ�˽���֪����㣬�����·������ȷ������෴����֪�յ��㣬�����·������֪�����յ㣬�������֮������·������ͼ���������·�����ܵó���ȷ�𰸣�


 ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪��ABC���������������ֱ�ΪA��-2��3����B��-6��0����C��-1��0����

��1����ֱ��д����A����ԭ��O�ԳƵĵ�����ꣻ
��2������ABC������ԭ��O��ʱ����ת90�������A��������ꡣ
��3����ֱ��д������A��B��CΪ�����ƽ���ı��εĵ��ĸ�����D������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����д�����չ��ɫ��ͨ������������ɫ��ͨ��ϵ����������������Ͷ��ʹ�ø����ǵij��д���������С����������������������ù����������ﳵʱ��t����λ���֣�������õ����ݷֳ����飬��������ͼͳ��ͼ�������ͼ����Ϣ������������⣺


��1�����������������______��
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У����ʾA�飨t��10�֣�������Բ�ĽǵĶ�����
��4������ﹲ��������ƽ���ٶ�Ϊ12km/h������㣬�����ù��������������У��ﳵ·�̲�����6km��������ռ�İٷֱȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У���A��x���ϣ�ֱ��OC�����еĵ�����![]() �����Ƕ�Ԫһ�η���
�����Ƕ�Ԫһ�η���![]() �Ľ⣬ֱ��AC�����еĵ�����
�Ľ⣬ֱ��AC�����еĵ�����![]() �����Ƕ�Ԫһ�η���
�����Ƕ�Ԫһ�η���![]() �Ľ⣬��C��x���ƽ���ߣ���y�����B��
�Ľ⣬��C��x���ƽ���ߣ���y�����B��
��1�����A��B��C�����ꣻ
��2����ͼ�ڣ���M��N�ֱ�Ϊ�߶�BC��OA�ϵ��������㣬��M�ӵ�C��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ��N�ӵ�O��ÿ��1��5����λ���ȵ��ٶ������˶������˶�ʱ��Ϊt�룬��0��t��4���ԱȽ��ı���MNAC��������ı���MNOB������Ĵ�С��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC�͡�ACB��ƽ�����ཻ�ڵ�O������O��EF��BC��AB��E����AC��F������O��OD��AC��D�������ĸ����ۣ�
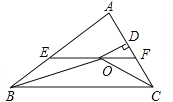
��EF=BE+CF��
�ڡ�BOC=90��+![]() ��A��
��A��
�۵�O����ABC���ߵľ�����ȣ�
����OD=m��AE+AF=n����![]() ��
��
������ȷ�Ľ�����____��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij����ɼס������Ӻ���12�������ɣ����蹤�̷���27720Ԫ���Ҷӵ���������������ʱ���Ǽӵ���������������ʱ���1.5�����Ҽ�ÿ��Ĺ��̷��ñ��ҶӶ�250Ԫ��
��1����ס������ӵ����������̸�������죿
��2�������̹������ž���������������ѡһ���ӵ�����ɴ���̣��ӽ�Լ�ʽ�ĽǶȿ��ǣ�Ӧѡ���ĸ����̶ӣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������y= ![]() x2ƽ�Ƶõ�������m��������m������A����6��0����ԭ��O��0��0�������Ķ���ΪP�����ĶԳ�����������y=
x2ƽ�Ƶõ�������m��������m������A����6��0����ԭ��O��0��0�������Ķ���ΪP�����ĶԳ�����������y= ![]() x2���ڵ�Q����ͼ����Ӱ���ֵ����Ϊ ��
x2���ڵ�Q����ͼ����Ӱ���ֵ����Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ���E��F�ֱ���BC��AB�ϣ���DE��AB��BE=AF��
��1����֤���ı���ADEF��ƽ���ı��Σ�
��2������ABC=60�㣬BD=4����ƽ���ı���ADEF�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com