
【题目】如图①,在平面直角坐标系中,点A在x轴上,直线OC上所有的点坐标![]() ,都是二元一次方程
,都是二元一次方程![]() 的解,直线AC上所有的点坐标
的解,直线AC上所有的点坐标![]() ,都是二元一次方程
,都是二元一次方程![]() 的解,过C作x轴的平行线,交y轴与点B.
的解,过C作x轴的平行线,交y轴与点B.
(1)求点A、B、C的坐标;
(2)如图②,点M、N分别为线段BC,OA上的两个动点,点M从点C以每秒1个单位长度的速度向左运动,同时点N从点O以每秒1.5个单位长度的速度向右运动,设运动时间为t秒,且0<t<4,试比较四边形MNAC的面积与四边形MNOB的面积的大小.

科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为CD上一点,DE:EC=2:3,连接AE,BE,BD,且AE,BD交于点F,则S△DEF:S△EBF:S△ABF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,有若干个点按如下规律排列:(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),…, 则第 200 个点的横坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y= ![]() x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.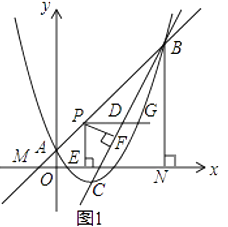
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+ ![]() BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+ ![]() BH的最小值;
BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y= ![]() x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K是直角三角形时,求t的值.
x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K是直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A,B两种花草每棵的价格分别是多少元?
(2)若购买A,B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光![]() ,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年的随机抽取了部分学生的鞋号,绘制了统计图A和图B,请根据相关信息,解答下列问题:
(1)本次随机抽样的学生数是多少?A中![]() 值是多少?
值是多少?
(2)本次调查获取的样本数据的众数和中位数各是多少?
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
①∠ABN=60°;②AM=1;③QN= ![]() ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是
;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是 ![]() .
.
其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建“美丽乡村”,某村计划购买甲、乙两种树苗共400棵,对本村道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.
![]() 若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
![]() 若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2 ![]() ,将扇形OAB沿过点B的直线折叠,点O恰好落在
,将扇形OAB沿过点B的直线折叠,点O恰好落在 ![]() 上的点D处,折痕交OA于点C,则阴影部分的面积是 .
上的点D处,折痕交OA于点C,则阴影部分的面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com