
����Ŀ����ƽ��ֱ������ϵ�У�����������y= ![]() ��x��0����ͼ������һ��A��a��3��������A��AB��x���ڵ�B������B��x��������ƽ��2����λ���ȵõ���C������C��y���ƽ���߽������������ڵ�D��CD=
��x��0����ͼ������һ��A��a��3��������A��AB��x���ڵ�B������B��x��������ƽ��2����λ���ȵõ���C������C��y���ƽ���߽������������ڵ�D��CD= ![]() ��ֱ��AD��x�ύ�ڵ�M����y�ύ�ڵ�N��
��ֱ��AD��x�ύ�ڵ�M����y�ύ�ڵ�N��
��1���ú�a��ʽ�ӱ�ʾ��D�ĺ�����Ϊ����
��2����a��ֵ��ֱ��AD�ĺ�������ʽ��
��3�����ж��߶�AN��MD��������ϵ����˵�����ɣ�
��4����һ�κ���y1=k1x+b1�����㣨10��9������˫����y= ![]() ��x��0�����ڵ�P���Ҹ�һ�κ���y1��ֵ��x�������������ȷ��P�������n��ȡֵ��Χ������д�����̣�
��x��0�����ڵ�P���Ҹ�һ�κ���y1��ֵ��x�������������ȷ��P�������n��ȡֵ��Χ������д�����̣�
���𰸡�
��1��a+2
��2���⣺��CD��y�ᣬ��CD= ![]() ��
��
��D��a+2�� ![]() ����
����
��A��D���ڷ���������ͼ���ϣ�
��  �����
����� ![]() ����a��ֵΪ2��
����a��ֵΪ2��
��A��2��3����D��4�� ![]() ����
����
��ֱ��AD�ĺ�������ʽΪy=kx+b��
��A��D���������ɵ� 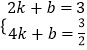 �����
�����  ��
��
��ֱ��AD�ĺ�������ʽΪy=�� ![]() x+
x+ ![]() ��
��
��3���⣺���ۣ�AN=MD��
���ɣ���y=�� ![]() x+
x+ ![]() �У���y=0�ɵ�x=6����x=0�ɵ�y=
�У���y=0�ɵ�x=6����x=0�ɵ�y= ![]() ��
��
��M��6��0����N��0�� ![]() ����
����
��A��2��3����D��4�� ![]() ����
����
��AN= ![]() =
= ![]() ��MD=
��MD= ![]() =
= ![]() ��
��
��AN=MD��
��4���⣺��ͼ����ֱ����x��ֱʱn��ֵ���ֱ����x��ƽ��ʱn��ֵ��С��

��ֱ�ߴ�ֱx��ʱ�����֪E�������Ϊ10������ʱn��ֵΪ10��
��ֱ��ƽ��x��ʱ����F���������Ϊ9���ɣ�1���ɵ÷�������������ʽΪy= ![]() ����y=9ʱ���ɽ��x=
����y=9ʱ���ɽ��x= ![]() ����P��ĺ�����Ϊ
����P��ĺ�����Ϊ ![]() ������ʱn��ֵΪ
������ʱn��ֵΪ ![]() ��
��
��һ�κ���y1��ֵ��x�����������
��ֱ����ֱ��P1E��ֱ��P2F֮�䣬
��n��ȡֵ��ΧΪ ![]() ��n��10��
��n��10��
���������⣺��1����A��a��3����AB��x���ڵ�B��
��OB=a��
�߽���B��x��������ƽ��2����λ���ȵõ���C��
��OC=OB+BC=2+a����D��ĺ�����Ϊa+2��
���Դ��ǣ�a+2��


 Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д� ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�������ABC�������ֱ��AP����C����ֱ��AP�ĶԳƵ�Ϊ��D������AD��BD������BD��ֱ��AP�ڵ�E.
��1�������ⲹȫͼ�Σ���2������PAC��20�㣬���AEB�Ķ�����
��3������CE��д��AE, BE, CE֮���������ϵ����֤����Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С��ͬѧ�������ʽa+2+ ![]() �Ĺ��̣�����ϸ�Ķ����������������⣮ a+2+
�Ĺ��̣�����ϸ�Ķ����������������⣮ a+2+ ![]() =2+a+
=2+a+ ![]() ����һ��
����һ��
=��2+a����2��a��+a2���ڶ���
=2��a2+a2��������
=2�����IJ�
��1��С���Ľⷨ�ӵ�����ʼ���ִ�����ȷ�Ļ���������
��2��ԭ����ʽ��ֵ�ܵ���2��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��ABCD�ı�CD���е㣬�ӳ�AE��BC���ӳ����ڵ�F��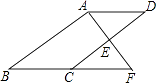
��1����֤����ADE�ա�FCE��
��2������BAF=90�㣬BC=5��EF=3����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ű��ΪA��B��C��D�Ŀ�Ƭ��������⣬������ȫ��ͬ��������ֱ�д����ͼ��ʾ���������泯�ϣ�ϴ�ȷźã��ִ��������ȡһ�ţ����Żأ����ٴ�ʣ�µĿ�Ƭ�������ȡһ�ţ� 
��1��������״ͼ���б��ķ�����ʾ���γ�ȡ��Ƭ�����п��ܳ��ֵĽ������Ƭ��A��B��C��D��ʾ����
��2������֪��������a2+b2=c2������������a��b��c��Ϊ����������鵽�����ſ�Ƭ�ϵ������ǹ������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC��һ�㣬����OB��OC������AB��OB��OC��AC���е�D��E��F��G�������ᣬ�õ��ı���DEFG��

��1����֤���ı���DEFG��ƽ���ı��Σ�
��2����MΪEF���е㣬OM=3����OBC����OCB���࣬��DG�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AOB=��BOC=��COD�����н����д�����ǣ�������

A. OB��OC�ֱ�ƽ��![]() ��
��![]()
B. ![]()
C. ![]()
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AO=CO��BO=DO���ҡ�ABC+��ADC=180�㣮
��1����֤���ı���ABCD�Ǿ��Σ�
��2������ADF����FDC=3��2��DF��AC�����BDF�Ķ����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABCD�У�E��F�ǶԽ���AC�����㣬����BE��BF��DE��DF��������������һ�����������ж��ı���BEDF�����Σ� �� 
A.��1=��2
B.BE=DF
C.��EDF=60��
D.AB=AF
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com