Question

【题目】如图，正方形ABCD的对角线相交于点O，BC=6，延长BC至点E，使得CE=8，点F是DE的中点，连接CF、OF．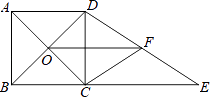

（1）求OF的长．
（2）求CF的长．

Answer 1

【答案】
（1）解：∵四边形ABCD是正方形，

∴BC=CD=6，∠BCD=∠ECD=90°，OB=OD，

∵CE=8，

∴BE=14，

∵OB=OD，DF=FE，

∴OF= BE=7．

（2）解：在Rt△DCE中，DE= = =10，

∵DF=FE，

∴CF= DE=5．

【解析】（1）由正方形的性质可知O为BD的中点，故此OF是△DBE的中位线，然后依据三角形中位线的性质解答即可；
（2）在Rt△DCE中，利用勾股定理求出DE，再利用直角三角形斜边上中线等于斜边的一半求解即可.
【考点精析】认真审题，首先需要了解正方形的性质(正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)．