
����Ŀ����ͥ����ҩƷ���ڡ�����Σ�շ����������������Ⱦ������Σ��������ij��ҩ�ಿ��Ϊ�˽������ͥ��������ҩƷ�ķ�ʽ��������ȫ�м�ͥ��һ�μ�����������ˣ�
��1������ѡȡ�����ķ����������һ���� ����ֻ��������ȷ�𰸵���ţ�
����������ij���������Լ�ͥΪ��λ�����ȡ������ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ������ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
��2�����γ������˷��֣����ܵ��˵ļ�ͥ���й���ҩƷ���ֽ��й����ݳ�����ͼ��

��m= ��n= ��
����ȫ����ͳ��ͼ��
�����ݵ������ݣ�����Ϊ���������ͥ��������ҩƷ����ķ�ʽ��ʲô��
����ͥ����ҩƷ����ȷ������ʽ���ͻ��յ㣬��������180��ͥ������ƴ�Լ�ж��ٻ���ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮
���𰸡���1��������2����20��6������ͼ����������B�ࣻ��18����
��������
�����������1�����ݳ�������ʱѡȡ����������д����Լ�����⣻
��2�������ȸ���A����80����ռ8%������������˵ļ�ͥ�ܻ���������D��������ܻ������m����E��������ܻ������n��
�����ܻ����ֱ��ȥA��B��D��E��F������õ�C��������ɲ�ȫ����ͳ��ͼ��
�����ݵ������ݣ�����֪�����������ͥ��������ҩƷ����ķ�ʽ��B�ࣻ
����180�����������ͻ��յ�Ļ�����ռ�ٷֱȼ��ɣ�
�����������1�����ݳ�������ʱѡȡ����������д����ԣ���֪����ѡȡ�����ķ����������һ��������
����������ij���������Լ�ͥΪ��λ�����ȡ������ȫ��ҽ���������Լ�ͥΪ��λ�����ȡ������ȫ�г�ס�˿����Լ�ͥΪ��λ�����ȡ��
��2�����������˵ļ�ͥ�ܻ���Ϊ��80��8%=1000��������m%=![]() =20%��m=20��n%=
=20%��m=20��n%=![]() =6%��n=6��
=6%��n=6��
�ʴ�Ϊ��20��6��
��C���Ϊ��1000����80+510+200+60+50��=100������ͳ��ͼ�������£�
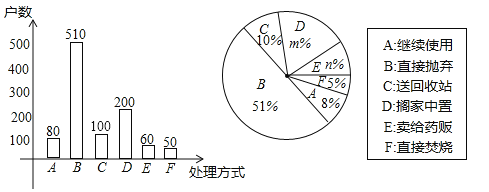
�����ݵ������ݣ�����֪�����������ͥ��������ҩƷ����ķ�ʽ��B�ࣻ
��180��10%=18������
��������180��ͥ�����ƴ�Լ��18��ͥ��������ҩƷ�ķ�ʽ���ͻ��յ㣮


 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���2x2��3x+1=0��������ǣ�������
A.����������ȵ�ʵ����
B.��������ȵ�ʵ����
C.ֻ��һ��ʵ����
D.û��ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ�ӱ�������ʽ�ֽ����(����)
A. x2��2x��3��x(x��2)��3
B. x2��2x��3��(x��1)2��4
C. (x��1)(x��3)��x2��2x��3
D. x2��2x��3��(x��1)(x��3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����÷ֽ���ʽ����57��99��44��99��99��ȷ����(����)��
A. 99��(57��44)��99��101��9 999 B. 99��(57��44��1)��99��100��9 900
C. 99��(57��44��1)��99��102��10 098 D. 99��(57��44��99)��99��2��198
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��B���߶�AD��һ���㣬��A��D�ķ�����2cm/s���ٶ��˶���C���߶�BD���е㣬AD=10cm.���B�˶���ʱ��Ϊt s.
��1����t=2 sʱ����AB= cm;
�����߶�CD�ij���.
![]()
��2�����˶������У����߶�AB���е�ΪE����EC�ij��Ƿ�仯�������䡣���EC�ij����������仯����˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
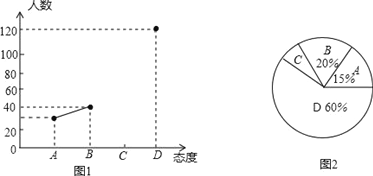
����Ŀ��Ŀǰ��ѧ�����ֻ���У����Խ��Խ�ܵ�����ע�������������ijУ��ѧ��ȤС���ͬѧ���������ѧУ�������ҳ��ԡ���ѧ�����ֻ��������̬�ȣ�̬�ȷ�Ϊ��A������ν��B�������ɣ�C���ɣ�D�����ԣ����������������Ƴ�Ƶ������ͳ��ͼ1������ͳ��ͼ2�����������������ͼ���ṩ����Ϣ������������⣺
��1���˴γ��������У��������˶�������ѧ���ҳ���
��2�����ͼ2������C���Ե�Բ�ĽǵĶ���������ͼ1����������
��3�����ݳ������������������1������ѧ���ҳ����ж������ҳ��ַ���̬�ȣ�
��4���ڴ˴ε����У�������1����ͳ�����2�������2λ�ҳ�����ѧ�����ֻ��ַ���̬�ȣ��ִ���4λ�ҳ���ѡ2λ�ҳ��μ�ѧУ��֯�ļ�У������б�������״ͼ�ķ�����ѡ����2�����Բ�ͬ�༶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=BC����ABC=90�㣬FΪAB�ӳ�����һ�㣬��E��BC�ϣ���AE=CF 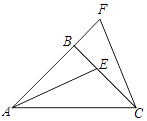
��1����֤����ABE�ա�CBF��
��2������BAE=25�㣬���ACF�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com