练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

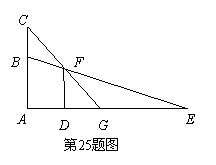
    如图所示，一只猫头鹰蹲在一棵树AC的B（点B在AC上）处，发现一只老鼠躲进短墙DF的另一侧，猫头鹰的视线被短墙遮住.为了寻找这只老鼠猫头鹰向上飞至树顶C处.DF=4米，短墙底部D与树的底部A间的距离为2.7米，猫头鹰从C点观察F点的俯角为53°，老鼠躲藏处M (点M在DE上)距D点3米.（参考数据：sin 37°≈0.60, cos 37°≈0.80，tan 37°≈0.75）

    (1)猫头鹰飞至C处后，能否看到这只老鼠？为什么？

    (2)要捕捉到这只老鼠，猫头鹰至少要飞多少米（精确到0.1米）？

     



    解：（1）由已知可得∠DFG=∠C=37°.

    在Rt△DFG中，DG=DF·tan 37°≈4×0.75=3(米).

    因此，猫头鹰能看到这只老鼠.

    （2）AG=AD+DG≈2.7+3=5.7（米），

    在Rt△ACG中，CG=≈9.5（米）.

    答：猫头鹰至少要飞9.5米.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    “嫦娥一号”返回探测数据表明：月球中午表面的温度是101度，半夜大约是-153度，中午比半夜高(     )

    A.52度     B.-52度     C.254度    D.-254度

    查看答案和解析>>

    科目：初中数学 来源： 题型：


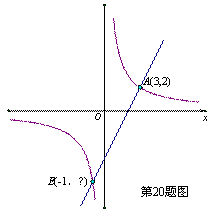
    如图所示，反比例函数y1的图象经过点A(3，2),解答下列问题：

    （1）求y1的函数关系式；

    （2）过y1上任意一点B向x轴，y轴作垂线，交两坐标轴于C，D两点,求矩形OCBD的面积;

    （3）过点A的一次函数y2与反比例函数y1

    的另一个交点E的横坐标为-1，求y2的关系式；

    （4）通过图象回答当x取何值时，y1>y2；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


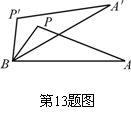
    如图所示，如果△APB绕点B按逆时针方向旋转30°后得到△A＇P＇B，且BP=2，那么点P与点P＇间的长度为___________． (不取近似值. 以下数据供解题使用：sin 15°=，cos 15°=)

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，在△ABC中，AD是BC边上的高，.

    （1）求证：AC＝BD;

    （2）若，求AD的长.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，∠C=90°，∠A，∠B，∠C的对边分别是a，b，c，且c-4ac+4a=0，则sinA+cosA的值为（  ）

        A．         D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一等腰三角形的两边长分别为4cm和6cm，则其底角的余弦值为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


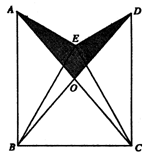
    如图，已知△BEC是等边三角形，∠AEB=∠DEC=90°．AE=DE，AC、BD的交点为O．

      （1）求证：△AEC≌△DEB；

      （2）若∠ABC=∠DCB=90°，AB=2cm，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图7，Rt△ABC中，∠ACB＝90°，AC＝4cm，AB＝5cm，点D是AB的中点，则cos∠ACD＝        ．

    查看答案和解析>>

    同步练习册答案