
如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°.AE=DE,AC、BD的交点为O.
(1)求证:△AEC≌△DEB;
(2)若∠ABC=∠DCB=90°,AB=2cm,求图中阴影部分的面积.
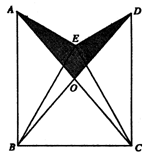
(1)证明略 (2)解:连结EO并延长EO交BC于点F,连结AD.
由(1),知AC=BD.∵∠ABC=∠DCB=90°,
∴∠ABC+∠DCB=180°,AB∥DC,AB=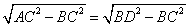 =CD,
=CD,
∴四边形ABCD为平行四边形且矩形.
∴OA=OB=OC=OD,又∵BE=CE,∴OE所在直线垂直平分线段BC,
∴BF=FC,∠EFB=90°,∴OF=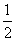 AB=
AB=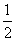 ×2=1,
×2=1,
∵△ BEC是等边三角形,∴∠EBC=60°,
BEC是等边三角形,∴∠EBC=60°,
在 Rt△AEB中,∠AEB=90°,∠ABE=∠ABC-∠EBC=90°-60°=30°,
Rt△AEB中,∠AEB=90°,∠ABE=∠ABC-∠EBC=90°-60°=30°,
∴BE=AB ·cos30°=2×
·cos30°=2×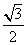 =
=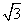 ,
,
在Rt△BFE中,∠BFE=90°,∠EBF=60 °,
°,
∴BF=BE·cos60°=
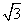 ×
×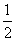 =
=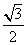 ,EF=BE·sin60°=
,EF=BE·sin60°=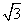 ×
×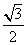 =
=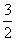 ,
,
∴OE=EF-OF=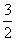 -1=
-1=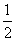 ,
,
∵AE=ED,OE=OE ,AO=DO,∴△AOE≌△DOE,
,AO=DO,∴△AOE≌△DOE,
∴S△AOE=S△DOE,
∴S阴影=2S△AOE =2×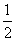 ·EO·BF=2×
·EO·BF=2×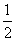 ×
×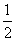 ×
×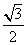 =
=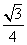 (cm2).
(cm2).


科目:初中数学 来源: 题型:
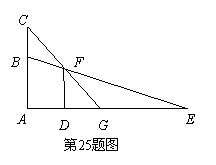
如图所示,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住.为了寻找这只老鼠猫头鹰向上飞至树顶C处.DF=4米,短墙底部D与树的底部A间的距离为2.7米,猫头鹰从C点观察F点的俯角为53°,老鼠躲藏处M (点M在DE上)距D点3米.(参考数据:sin 37°≈0.60, cos 37°≈0.80,tan 37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米 )?
)?
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,梯形ABCD中,AD∥BC,∠B=45°,∠D=120°,AB=6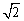 cm,则DC的长为 ( )
cm,则DC的长为 ( )
 A.2
A.2 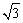 cm B.
cm B. 2
2 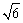 cm C.4 cm D.4
cm C.4 cm D.4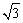 cm
cm

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com