
在△ABC内侧作射线 ,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.
,自B,C分别向射线AP引垂线,垂足分别为D,E,M为BC边中点,连接MD,ME.
(1)依题意补全图1;
(2)求证:MD=ME;
(3)如图2,若射线AP平分∠BAC,且AC>AB,求证:MD=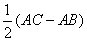 .
.
 | |||
 | |||
解:(1)补全图形,如图1所示. ……… 1分
(2)延长DM交CE于点F.
∵BD、CE分别垂直AP于点D、E.
∴BD∥CE.,∴∠1= ∠2.
∵M为BC边中点,
∴BM=CM, 又∵∠DMB= ∠FMC,
∴△DMB≌△FMC (ASA),
∴DM=FM.
∵∠DEF=90°.
∴EM=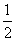 DF,
DF,
∴MD=ME.
 | |||
 | |||
(3)延长BD交AC于点G.
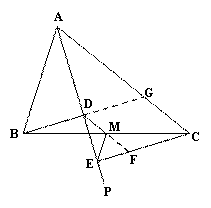 ∵BD⊥AP于点D,射线AP平分∠BAC,
∵BD⊥AP于点D,射线AP平分∠BAC,
∴△ADB≌△ADG (ASA),
∴BD=DG,AB=AG.
又∵△DMB≌△FMC,
∴BD=CF,DM=MF,
∴CF=DG,
又∵BG∥CF,
∴四边形DFCG为平行四边形.
∴DF=CG,
∴2MD=CG,
∴2MD=AC-AB,
∴MD=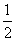 (AC-AB).
(AC-AB).


科目:初中数学 来源: 题型:
对某一种四边形给出如下定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.则∠C= 度,∠D=  度.
度.
(2)在探究“等对角四边形”性质时:
小红画了一个“等对角四边形ABCD”(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
(3)已知:在“等对角 四边形ABCD”中,∠DAB=60°,
四边形ABCD”中,∠DAB=60°, ∠ABC=90°,AB=5,AD=4.求对角线AC的长.
∠ABC=90°,AB=5,AD=4.求对角线AC的长.
 | |||
 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.
(1)求证:PB+PC>2AB.
(2)当PC=2,PB= ,∠ACP=45°时,求AB的长.
,∠ACP=45°时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
.阅读理解并填空:
(1)为了求代数式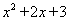 的值,我们必须知道
的值,我们必须知道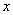 的值.若
的值.若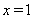 ,则这个代数式的值为_______;若
,则这个代数式的值为_______;若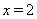 ,则这个代数式的值为__
,则这个代数式的值为__ _____,……,可见,这个代数式的值因
_____,……,可见,这个代数式的值因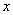 的取值不同而_______(填“变化”或“不变”).尽管如此,我们还是有办法来考虑这个代数式的值的范围.
的取值不同而_______(填“变化”或“不变”).尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)把一个多项式进行部分因式分解可以来解决代数式值的最大(或最小)值问题.例如: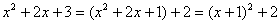 ,因为
,因为 是非负数,所以,这个代数式
是非负数,所以,这个代数式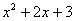 的最小值是_______,这时
的最小值是_______,这时 相应的
相应的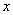 的值是__________.
的值是__________.
尝试探究并解答:
(3)求代数式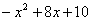 的最大(或最小)值,并写出相应的
的最大(或最小)值,并写出相应的
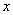 的值.
的值.
(4)求代数式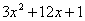 的最大(或最小)值,并写出相应的
的最大(或最小)值,并写出相应的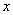 的值.
的值.
(5)已知 ,且
,且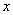 的值在数1~4(包含1和4)之间变化,求这时
的值在数1~4(包含1和4)之间变化,求这时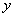 的变化范围.
的变化范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com