Question

13．如图1，在正方形ABCD的外部，分别以AB，CD为边作菱形ABEF和菱形CDGH，连接EH，FG
（1）求证：FG=EH
（2）请从A，B两个题目中任选一题作答
A  如图2，若AB=4，∠BAF=60°，∠CDG=30°，求四边形AFGD的面积
B   如图3，若∠BAF=∠CDG，求证；四边形EFGH是矩形

Answer 1

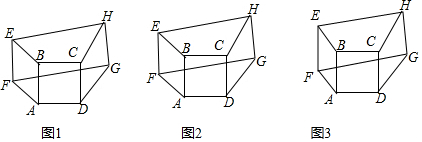
分析 （1）由四边形ABEF是菱形得出AB∥EF，AB=EF，同理得出CD∥HG，CD=HG，而AB∥CD，AB=CD，即可得出EF∥HG，EF=HG即可得出结论；
（2）A、延长FA，GD构造出直角三角形，利用含30°的直角三角形的性质求出AM，DM，进而得出MF，MG，最后用大直角三角形的面积减去小直角三角形的面积即可．
B、方法1、先判断出△ADF≌△DAG，得出∠ADF=∠DAG，再判断出△AFG≌△DGF得出∠DFG=∠AGF，借助对顶角得出∠ADF=∠DFG进而得出AD∥FG即可得出结论．
方法2、先判断出MF=MG，∠AFE=∠DGH，进而判断出∠EFG=∠HGF，再判断出∠EFG+∠HGF=180°，即可得出结论．

解答 解：（1）∵AB，CD为边作菱形ABEF和菱形CDGH，
∴EF∥AB，EF=AB，HG∥CD，HG=CD，
∵四边形ABCD是正方形，
∴AB∥CD，AB=CD，
∴EF∥HG，EF=HG，
∴四边形EFGH是平行四边形，
∴FG=EH；
（2）A、如图2，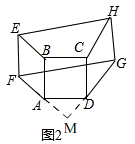

延长FA，GD交于M，
∵四边形ABCD是正方形，
∴∠BAD=∠ADC=90°，
∴∠BAF+∠DAM=90°，∠CDG+∠ADM=90°，
∵∠BAF=60°，∠CDG=30°，
∴∠DAM=30°，∠ADM=60°，
∴∠ADM=180°-∠DAM-∠ADM=90°
在Rt△ADM中，∠DAM=30°，AD=4，
∴DM=$\frac{1}{2}$AD=2，AM=2$\sqrt{3}$，
∵AF=DG=4，
∴FM=AF+AM=4+2$\sqrt{3}$，MG=MD+DG=6，
∴S_{四边形AFGD}=S_△FMG-S_△MAD
=$\frac{1}{2}$×FM×GM-$\frac{1}{2}$×AM×DM=$\frac{1}{2}$×（4+2$\sqrt{3}$）×6-$\frac{1}{2}$×2$\sqrt{3}$×2=12+4$\sqrt{3}$，
B、方法1、如图3．连接FD，AG（简化图），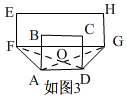

∵∠BAF=∠CDG，
∴∠DAF=∠ADG
在△ADF和△ADG中，$\left\{\begin{array}{l}{AD=AD}\\{∠DAF=∠ADG}\\{AF=DG}\end{array}\right.$，
∴△ADF≌△ADG，
∴∠ADF=∠DAG，DF=AG，
∴∠ADF=$\frac{1}{2}$（180°-∠AOD）
在△AFG和△DGF中，$\left\{\begin{array}{l}{AF=DG}\\{AG=DF}\\{FG=GF}\end{array}\right.$，
∴△AFG≌△DGF，∠AGF=∠DFG，
∴∠DFG=$\frac{1}{2}$（180°-∠FOG）
∵∠FOG=∠AOD，
∴∠ADF=∠DFG，
∴AD∥FG，
∵AB⊥AD，
∴AB⊥FG，
∵AB∥EF，
∴EF⊥FG，
∴∠EFG=90°，
由（1）知，四边形EFGH为平行四边形，
∴平行四边形EFGH是矩形，
即：四边形EFGH是矩形．

方法2、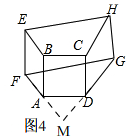
延长FA，GD交于M，
∵四边形ABCD是正方形，
∴∠BAD=∠ADC=90°，
∵∠BAF=∠CDG，
∴∠MAD=∠MDA，
∴MA=MD，
∵四边形ABCD是正方形，
∴AB=CD，
∵四边形ABEF，CDGH是菱形，
∴MF=MG，∠AFE=∠DGH，
∴∠EFG=∠HGF，
由（1）知，四边形EFGH是平行四边形，
∴∠AFE+∠HGF=180°，
∴∠EFG=90°，
∴平行四边形EFGH是矩形．

点评 此题是四边形综合题，主要考查了正方形的性质，菱形的性质全等三角形的判定和性质，矩形的判定，解本题的关键是分清特殊四边形的性质和判定，难点是（3）图形的分解．