
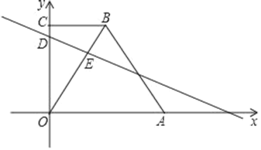
【题目】在平面直角坐标系中,BC∥OA,BC=3,OA=6,AB=3![]() .
.
(1)直接写出点B的坐标;
(2)已知D、E(2,4)分别为线段OC、OB上的点,OD=5,直线DE交x轴于点F,求直线DE的解析式;
(3)在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)B(3,6);(2)y=﹣![]() x+5;(3)见解析.
x+5;(3)见解析.
【解析】
(1)过B作BG⊥OA于点G,在Rt△ABG中,利用勾股定理可求得BG的长,则可求得B点坐标;
(2)由条件可求得D点坐标,利用待定系数法可求得直线DE的解析式;
(3)当OD为边时,则MO=OD=5或MD=OD=5,可求得M点坐标,由MN∥OD,且MN=OD可求得N点坐标;当OD为对角线时,则MN垂直平分OD,则可求得M、N的纵坐标,则可求得M的坐标,利用对称性可求得N点坐标.
解:(1)如图1,过B作BG⊥OA于点G,
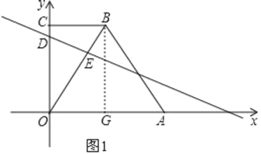
∵BC=3,OA=6,
∴AG=OA﹣OG=OA﹣BC=6﹣3=3,
在Rt△ABG中,由勾股定理可得AB2=AG2+BG2,即(3![]() )2=32+BG2,解得BG=6,
)2=32+BG2,解得BG=6,
∴OC=6,
∴B(3,6);
(2)由OD=5可知D(0,5),
设直线DE的解析式是y=kx+b
把D(0,5)E(2,4)代入得![]() ,解得:
,解得: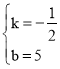 ,
,
∴直线DE的解析式是y=﹣![]() x+5;
x+5;
(3)当OD为菱形的边时,则MN=OD=5,且MN∥OD,
∵M在直线DE上,
∴设M(t,﹣![]() t+5),
t+5),
①当点N在点M上方时,如图2,则有OM=MN,

∵OM2=t2+(﹣![]() t+5)2,
t+5)2,
∴t2+(﹣t+5)2=52,解得t=0或t=4,
当t=0时,M与D重合,舍去,
∴M(4,3),
∴N(4,8);
②当点N在点M下方时,如图3,则有MD=OD=5,
∴t2+(﹣![]() t+5﹣5)2=52,解得t=2
t+5﹣5)2=52,解得t=2![]() 或t=﹣2
或t=﹣2![]() ,
,
当t=2![]() 时,N点在x轴下方,不符合题意,舍去,
时,N点在x轴下方,不符合题意,舍去,
∴M(﹣2![]() ,
,![]() +5),
+5),
∴N(﹣2![]() ,
,![]() );
);
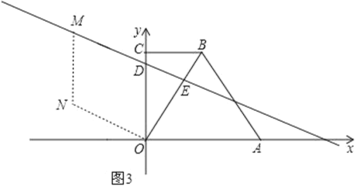
当OD为对角线时,则MN垂直平分OD,
∴点M在直线y=2.5上,
在y=﹣![]() x+5中,令y=2.5可得x=5,
x+5中,令y=2.5可得x=5,
∴M(5,2.5),
∵M、N关于y轴对称,
∴N(﹣5,2.5),
综上可知存在满足条件的点N,其坐标为(4,8)或(﹣5,2.5)或(﹣2![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,某勘测队在一条近似笔直的河流l两边勘测(河宽忽略不计),共设置了A,B,C三个勘测点.
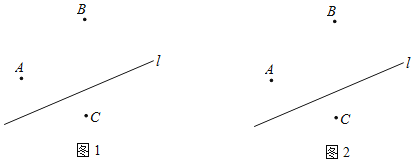
(1)若勘测队在A点建一水池,现将河水引入到水池A中,则在河岸的什么位置开沟,才能使水沟的长度最短?请在图1中画出图形;你画图的依据是 .
(2)若勘测队在河岸某处开沟,使得该处到勘测点B,C所挖水沟的长度之和最短,请在图2中画出图形;你画图的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,与
,与![]() 互为余角,与
互为余角,与![]() 互为补角,
互为补角,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,

(1)如图,当![]() 时,求
时,求![]() 的度数;
的度数;
(2)在(1)的条件下,请你补全图形,并求![]() 的度数;
的度数;
(3)当![]() 为大于
为大于![]() 的锐角,且
的锐角,且![]() 与
与![]() 有重合部分时,请求出
有重合部分时,请求出![]() 的度数.(写出说理过程,用含
的度数.(写出说理过程,用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子).下列叙述正确的是( )
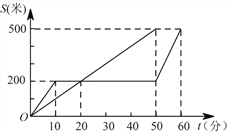
A. 赛跑中,兔子共休息了50分钟
B. 乌龟在这次比赛中的平均速度是0.1米/分钟
C. 兔子比乌龟早到达终点10分钟
D. 乌龟追上兔子用了20分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
【答案】1
【解析】试题分析:把原式的第一项根据负整数指数幂的意义化简,第二项根据算术平方根的定义求出9的算术平方根,第三项根据零指数公式化简,最后一项利用特殊角的三角函数值化简,合并后即可求出值.
试题解析:原式=4﹣3+1﹣![]()
=2﹣1
=1.
【题型】解答题
【结束】
16
【题目】《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() .
.
(1)请用尺规按下列要求作图:
①作线段![]() ;
;
②在线段![]() 的延长线上顺次截取
的延长线上顺次截取![]() ;
;
(2)在(1)所作的图中,若点![]() 是线段
是线段![]() 的中点,
的中点,![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 为整数
为整数
(1)![]() 能取最 (填“大”或“小”)值是 .此时
能取最 (填“大”或“小”)值是 .此时![]() = .
= .
(2)![]() +2能取最 (填“大”或“小”)值是 .此时
+2能取最 (填“大”或“小”)值是 .此时![]() = .
= .
(3)![]() 能取最 (填“大”或“小”)值是 .此时
能取最 (填“大”或“小”)值是 .此时![]() = .
= .
(4)![]() 能取最 (填“大”或“小”)值是 . 此时
能取最 (填“大”或“小”)值是 . 此时![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接省“义务教育均衡发展验收”,某广告公司承担了制作宣传牌任务,安排甲、乙两名工人制作,由于乙工人采用了新式工具,其工作效率比甲工人提高了20%,同样制作30个宣传牌,乙工人比甲工人节省了一天时间:
(1)求甲乙两名工人每天各制作多少个宣传牌?
(2)现在需要这两名工人合作完成44个宣传牌制作在务,应如何分配,才能让两名工人同时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
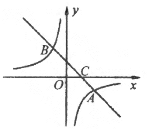
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于
的图像交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)将![]() 轴下方的图像沿
轴下方的图像沿![]() 轴翻折,点
轴翻折,点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com