
分析 (1)利用负整数指数幂的意义化简a,利用分母有理化的知识化简b,根据零指数幂的意义化简c,根据绝对值的意义化简d,利用算术平方根的意义化简e,进而求解即可;
(2)原式第一项通分后,再将除法转化为乘法,将分式化为最简,然后把x=-4代入计算即可.
解答 解:(1)a=($\frac{1}{3}$)-1=3,b=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1,c=(2014-π)0=1,d=|1-$\sqrt{2}$|=$\sqrt{2}$-1,e=$\sqrt{4}$=2,
bd+a-e=($\sqrt{2}$+1)($\sqrt{2}$-1)+3-2
=1+3-2
=2;
(2)原式=($\frac{x-1}{x-1}$+$\frac{1}{x-1}$)÷$\frac{x}{{x}^{2}-1}$
=$\frac{x}{x-1}$•$\frac{(x+1)(x-1)}{x}$
=x+1,
当x=-4时,
原式=-4+1=-3.
点评 本题考查了分式的化简求值,解答此题的关键是把分式化到最简,然后代值计算.同时考查了负整数指数幂的意义,分母有理化,零指数幂的意义,绝对值的意义以及算术平方根的意义.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:解答题
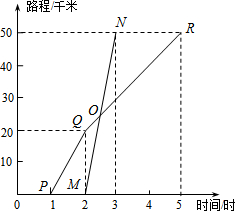 已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:
已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.
2015年3月全国两会期间,民生活题成为了社会关注的焦点,成都商报为了了解百姓“两会民生活题”的聚焦点,记者随机调查了成都市部分市民,并对调查进行整理,绘制成了如图所示的不完整的统计图表.| 组别 | 焦点话题 | 频数(人数) |
| A | 延迟退休 | 120 |
| B | 汽车尾号限行 | 80 |
| C | 就业养老 | m |
| D | 教育医疗 | n |
| E | 生态环保 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3和-1之间的有理数是-2 | |
| B. | 数轴上表示-a的点一定在原点的左边 | |
| C. | 在数轴上离开原点的距离越近的点表示的数越小 | |
| D. | -1和-2之间有无数个负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
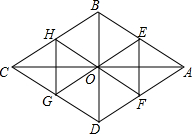 如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.
如图,四边形ABCD是菱形,对角线AC=8,BD=6,E,F分别是AB,AD的中点,连接EO并延长交CD于G点,连接FO并延长交CB于H点,△OEF与△OGH组成的图形称为蝶形,则蝶形的周长为16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
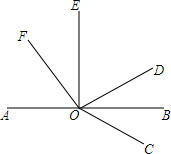 如图.点O是直线AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC.
如图.点O是直线AB上一点,∠AOE是直角,∠FOD=90°,OB平分∠DOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
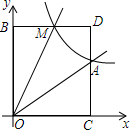 已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).
已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com