练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．已知x=$\frac{{4-\sqrt{7}}}{3}$，则$\frac{x^2}{{{x^4}+{x^2}+1}}$=$\frac{9}{55}$．

    分析 先化简，再把x=$\frac{{4-\sqrt{7}}}{3}$代入求值．

    解答 解：$\frac{x^2}{{{x^4}+{x^2}+1}}$=$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$=$\frac{1}{（x+\frac{1}{x}）^{2}-1}$，
    当x=$\frac{{4-\sqrt{7}}}{3}$，原式=$\frac{1}{（\frac{4-\sqrt{7}}{3}+\frac{3}{4-\sqrt{7}}）^{2}-1}$=$\frac{1}{（\frac{8}{3}）^{2}-1}$=$\frac{9}{55}$．
    故答案为：$\frac{9}{55}$．

    点评 本题主要考查了分式的化简求值，解题的关键是正确的计算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    20．某机关单位2015年3月的三公经费为a万元，为响应省委提倡节俭的号召，开始减少三公经费，4月份比3月份减少10%，5月份又比4月份减少15%，则5月份的三公经费是（1-10%）（1-15%）a万元（用含a的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．若不等式$\left\{\begin{array}{l}x-a＞0\\ x＜a+1\end{array}\right.$的解集中任一个x的值均不在2≤x≤5的范围内，则a的取值范围是a≥5或a≤1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列函数中和函数$y=\frac{1}{x-1}$的图象关于y轴对称的（　　）
    A．$y=\frac{1}{x+1}$B．$y=-\frac{1}{x+1}$C．$y=\frac{1}{1-x}$D．$y=\frac{1}{x-1}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．在直角三角形ABC中，∠C=90°，AD是∠A的平分线，且CD=$\sqrt{6}$，DB=$2\sqrt{6}$，求△ABC的三边长？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

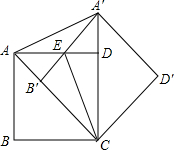    15．如图，把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′（此时，点B′落在对角线AC上，点A′落在CD的延长线上），A′B′交AD于点E，连接AA′、CE．求证：AA′=CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知等边三角形边长为a，点O是△ABC的重心，求AO，OD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

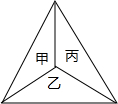    19．如图，一只蚊子在甲、乙、丙三个房间之间飞来飞去，蚊子从一个房间随机飞到另一个房间，共飞三次．
    （1）若开始时蚊子在甲房间，求经过三次飞行后，蚊子回到甲房间的概率是多少？
    （2）若想使蚊子经过三次飞行后回到乙房间的概率最大，则蚊子最开始时在哪个房间？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．化简：$\frac{1}{1+x}$+$\frac{2x}{1-{x}^{2}}$．

    查看答案和解析>>

    同步练习册答案