练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如果点A、B关于X轴对称，点B、C关于Y轴对称，那么点A、C


    1. A.
      是重合
    2. B.
      关于X轴对称
    3. C.
      关于Y轴对称
    4. D.
      关于原点对称
    D
    分析：根据平面直角坐标系内关于x轴、y轴对称的点的特点，先设出A点坐标依次得出B、C点坐标，即可得出答案．
    解答：设A点坐标为（a，b），
    ∵点A、B关于X轴对称，
    ∴点B坐标为（a，-b），
    ∵点B、C关于Y轴对称，
    ∴点C坐标为（-a，-b），
    ∴点A、C关于原点对称．
    故选D．
    点评：本题主要考查了平面直角坐标系内关于x轴、y轴及原点对称的点的特点，难度适中．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2011•岳池县模拟）如图，在平面直角坐标系xoy中，已知抛物线顶点N的坐标为（-1．-
    92
    ），此抛物线交y轴于B（0，-4），交x轴于A、C两点且A点在C点左边．
    （1）求抛物线解析式及A、C两点的坐标．
    （2）如果点M为第三象限内抛物线上一个动点且它的横坐标为m，设△AMB的面积为S，求S关于m的函数关系式并求出S的最大值．
    （3）若点P是抛物线上的动点，点Q是直线y=x上的动点，判断有几个位置使得以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知点P（x，y）、Q（m，n），如果x+m=0，y-n=0，那么点P、Q关于
    y轴
    y轴
    对称．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    作一个图形关于一条直线的轴对称图形，再将这个轴对称图形沿着与这条直线平行的方向平移，我们把这样的图形变换叫做关于这条直线的滑动对称变换．在自然界和日常生活中，大量地存在这种图形变换（如图1），结合轴对称和平移的有关性质，解答以下问题：精英家教网
    （1）如图2，在关于直线l的滑动对称变换中，试证明：两个对应点A，A′的连线被直线l平分；
    （2）若点P是正方形ABCD的边AD上的一点，点P关于对角线AC滑动对称变换的对应点P′也在正方形ABCD的边上，请仅用无刻度的直尺在图3中画出P′；
    （3）定义：若点M到某条直线的距离为d，将这个点关于这条直线的对称点N沿着与这条直线平行的方向平移到点M′的距离为s，称[d，s]为点M与M′关于这条直线滑动对称变换的特征量．如图4，在平面直角坐标系xOy中，点B是反比例函数y=
    3x
    的图象在第一象限内的一个动点，点B关于y轴的对称点为C，将点C沿平行于y轴的方向向下平移到点B′．
    ①若点B（1，3）与B′关于y轴的滑动对称变换的特征量为[m，m+4]，判断点B′是否在此函数的图象上，为什么？
    ②已知点B与B′关于y轴的滑动对称变换的特征量为[d，s]，且不论点B如何运动，点B′也都在此函数的图象上，判断s与d是否存在函数关系？如果是，请写出s关于d的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源：新教材新学案　数学　八年级上册 题型：013

    如果P(2，3)关于y轴的对称点为，则的坐标为

    [　　]

    A．(2，－3)

    B．(－2，3)

    C．(－2，－3)

    D．(2，3)

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    画出一个平面直角坐标系，在坐标平面内描出下列各点：

    A(－1，5)，B(－4，2)，C(5，2)，D(8，5)．

    (1)将A，B，C，D依次用线连结成封闭图形，你会得到一个什么样的图形？它是轴对称图形吗？如果是，请你画出它的对称轴．

    (2)作出点C，D关于x轴的对称点，，将C，D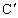，，依次用线连结起来，你又会得到一个什么样的封闭图形？它是轴对称图形吗？如果是，请你画出它的对称轴．

    (3)若把四边形ABCD沿y轴翻折，写出各对应点的坐标．

    查看答案和解析>>

    同步练习册答案