
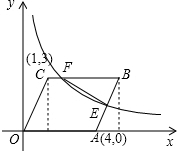
 在直角坐标系中A点坐标为(4,0),C点坐标为(1,3)
在直角坐标系中A点坐标为(4,0),C点坐标为(1,3)分析 (1)作CM⊥x轴,BN⊥x轴分别于点M和N,则△OCM≌△ABN,则OM=AN,据此即可求得B的坐标;
(2)根据E是AB的中点,即可求得E的坐标,然后把E代入反比例函数解析式,即可求得k;
(3)作FG⊥x轴,EH⊥x轴分别于点G和H,根据S五边形OAEFC=S梯形OGFC+S梯形FGHE-S△AHE即可求解.
解答 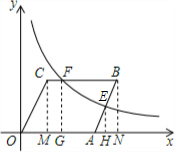 解:(1)作CM⊥x轴,BN⊥x轴分别于点M和N.则△OCM≌△ABN,则OM=AN=1,ON=4+1=5.
解:(1)作CM⊥x轴,BN⊥x轴分别于点M和N.则△OCM≌△ABN,则OM=AN=1,ON=4+1=5.
则B的坐标是(5,3);
(2)∵E是AB的中点,
∴E的坐标是($\frac{9}{2}$,$\frac{3}{2}$).
把E的坐标代入y=$\frac{k}{x}$得:k=$\frac{9}{2}$×$\frac{3}{2}$=$\frac{27}{4}$;
(3)反比例函数的解析式是:y=$\frac{27}{4x}$,
令y=3,则3=$\frac{27}{4x}$,解得:x=$\frac{9}{4}$,
则F的坐标是($\frac{9}{4}$,3).
作FG⊥x轴,EH⊥x轴分别于点G和H.
则G的坐标是($\frac{9}{4}$,0),H的坐标是($\frac{9}{2}$,0),
S梯形OGFC=$\frac{1}{2}$(CF+OG)•FG=$\frac{1}{2}$×($\frac{5}{4}$+$\frac{9}{4}$)×3=$\frac{39}{8}$,
S梯形FGHE=$\frac{1}{2}$(GF+EH)•GH=$\frac{1}{2}$×(3+$\frac{3}{2}$)×$\frac{9}{4}$=$\frac{81}{16}$,
S△AHE=$\frac{1}{2}$AH•EH=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{3}{2}$=$\frac{3}{8}$,
则S五边形OAEFC=S梯形OGFC+S梯形FGHE-S△AHE=$\frac{39}{8}$+$\frac{81}{16}$-$\frac{3}{8}$=$\frac{153}{16}$.
点评 本题考查了待定系数法求反比例函数解析式,以及图形面积的计算,正确作出辅助线,连接S五边形OAEFC=S梯形OGFC+S梯形FGHE-S△AHE是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
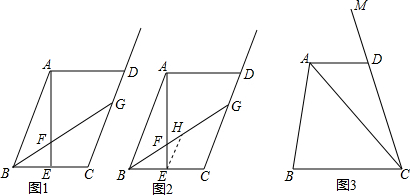
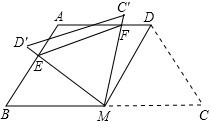 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.将△MDC绕点M旋转,旋转后对应的三角形为△MC′D′,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,连接EF,求证:EF∥C′D′.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.将△MDC绕点M旋转,旋转后对应的三角形为△MC′D′,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,连接EF,求证:EF∥C′D′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
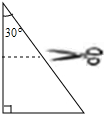 如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.
如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5y2-2y2=3 | B. | x6+x2=x8 | C. | (-a-b)2=a2-2ab+b2 | D. | $\sqrt{27}$-$\sqrt{12}$=$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com