
【题目】在平面直角坐标系xOy中,已知正比例函数的图象与反比例函数![]() 的图象交于点A(m,4).
的图象交于点A(m,4).
(1)求正比例函数的解析式;
(2)将正比例函数的图象向下平移6个单位得到直线l,设直线l与x轴的交点为B,求∠ABO的正弦值.
【答案】(1)y=2x;(2)![]()
【解析】
(1)由于点A经过(m,4)所以可求出m=2,再将A(2,4)代入反比例函数中即可求出k的值.
(2)先求平移后的直线l的解析式,然后求出B的坐标,利用勾股定理可求出AB的长度,利用正弦的定义即可求出∠ABO的正弦值.
(1)∵反比例函数![]() 的图象经过A(m,4),
的图象经过A(m,4),
∴![]() ,解得m=2.
,解得m=2.
∴点A的坐标为(2,4).
设正比例函数的解析式为y=kx,
∵正比例函数的图象经过点A(2,4),
∴可得 4=2k,解得k=2.
∴正比例函数的解析式是y=2x
(2)∵正比例函数向下平移6个单位得到直线l,
∴直线l的表达式为y=2x﹣6
∵直l与x轴的交点为B,
∴点B的坐标是(3,0)
∴由勾股定理可知:![]() .
.
∴![]()


科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D,E分别为△ABC的边AB,BC上两点,点A,C,E在⊙D上,点B,D在⊙E上.F为![]() 上一点,连接FE并延长交AC的延长线于点N,交AB于点M.
上一点,连接FE并延长交AC的延长线于点N,交AB于点M.
(1)若∠EBD为α,请将∠CAD用含α的代数式表示;
(2)若EM=MB,请说明当∠CAD为多少度时,直线EF为⊙D的切线;
(3)在(2)的条件下,若AD=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
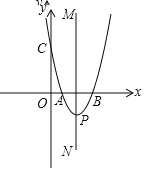
【题目】平面直角坐标系xOy(如图),抛物线y=﹣x2+2mx+3m2(m>0)与x轴交于点A、B(点A在点B左侧),与y轴交于点C,顶点为D,对称轴为直线l,过点C作直线l的垂线,垂足为点E,联结DC、BC.
(1)当点C(0,3)时,
①求这条抛物线的表达式和顶点坐标;
②求证:∠DCE=∠BCE;
(2)当CB平分∠DCO时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,与y轴相交于点C,顶点为P.
,与y轴相交于点C,顶点为P.
(1)求这条抛物线的表达式和顶点P的坐标;
(2)点E在抛物线的对称轴上,且![]() ,求点E的坐标;
,求点E的坐标;
(3)在(2)的条件下,记抛物线的对称轴为直线MN,点Q在直线MN右侧的抛物线上,![]() ,求点Q的坐标.
,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,连接AD交线段PQ于点E,且![]() ,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
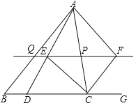
(1)求证:PC=PE;
(2)当P是边AC的中点时,求证:四边形AECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点P是AC边上的一点,过点P作与BC平行的直线PQ,交AB于点Q,点D在线段 BC上,连接AD交线段PQ于点E,且![]() ,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.
,点G在BC延长线上,∠ACG的平分线交直线PQ于点F.

(1)求证:PC=PE;
(2)当P是边AC的中点时,求证:四边形AECF是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1,如果点B1落在射线BD上,那么CC1的长度为_____.
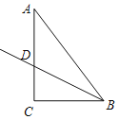
查看答案和解析>>
科目:初中数学 来源: 题型:
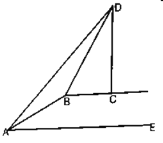
【题目】如图,在坡顶![]() 处的同一水平面上有一座纪念碑
处的同一水平面上有一座纪念碑![]() 垂直于水平,小明在斜坡底
垂直于水平,小明在斜坡底![]() 处测得该纪念碑顶部
处测得该纪念碑顶部![]() 的仰角为
的仰角为![]() ,然后他沿着坡比
,然后他沿着坡比![]() 的斜坡
的斜坡![]() 攀行了39米到达坡顶,在坡顶
攀行了39米到达坡顶,在坡顶![]() 处又测得该纪念碑顶部的仰角为
处又测得该纪念碑顶部的仰角为![]() .求纪念碑
.求纪念碑![]() 的高度.(结果精确到1米,参考数据:
的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com