练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为了迎接春节，某县准备用灯笼美化滨河路，许采用A、B两种不同造型的灯笼共600个．且A型灯笼的数量比B型灯笼的多15个．

    （1）求A、B两种灯笼各需多少个？

    （2）已知A、B型灯笼的单价分别为40元、30元，则这次美化工程需多少费用？

    【答案】（1）A型灯笼需249个；B型灯笼需351个；（2）美化工程需20490元．

    【解析】

    试题分析：（1）设B型灯管需x个，则A型需（x+15）个，根据A、B两种不同造型的灯笼共600个即可列方程求解；

    （2）根据单价乘以数量即可求得费用，据此即可求解．

    解：（1）设B型灯管需x个，则A型需（x+15）个．

    根据题意得x+（x+15）=600，

    解得：x=351，

    则A型灯笼需×351+15=249（个）；

    （2）249×40+351×30=20490（元）．

    答：A型灯笼需249个，B型灯笼需351个，这次美化工程需20490元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】用直尺和圆规作一个角等于已知角的示意图如下，则说明∠A′O′B′=∠AOB的依据是（ ）

    A．（S．S．S．） B．（S．A．S．） C．（A．S．A．） D．（A．A．S．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB、CD相交于点O，OF平分∠AOE，OF⊥CD，垂足为O．

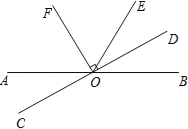
    （1）若∠AOE=120°，求∠BOD的度数；

    （2）写出图中所有与∠AOD互补的角： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2016年春节期间，在网络上用“百度”搜索引擎搜索“开放二孩”，能搜索到与之相关的结果个数约为45100000，这个数用科学记数法表示为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们规定：函数y=（a、b、k是常数，k≠ab）叫奇特函数．当a=b=0时，奇特函数y=就是反比例函数y=（k是常数，k≠0）．

    （1）如果某一矩形两边长分别是2和3，当它们分别增加x和y后，得到新矩形的面积为8．求y与x之间的函数表达式，并判断它是否为奇特函数；

    （2）如图，在平面直角坐标系xOy中，矩形OABC的顶点A、C坐标分别为（6，0）、（0，3），点D是OA中点，连接OB、CD交于E，若奇特函数y=的图象经过点B、E，求该奇特函数的表达式；

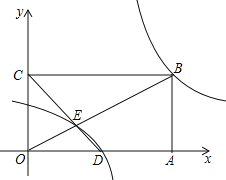
    （3）把反比例函数y=的图象向右平移4个单位，再向上平移 个单位就可得到（2）中得到的奇特函数的图象；

    （4）在（2）的条件下，过线段BE中点M的一条直线l与这个奇特函数图象交于P，Q两点（P在Q右侧），如果以B、E、P、Q为顶点组成的四边形面积为16，请直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，x=﹣1是对称轴，有下列判断：①b﹣2a=0；②4a﹣2b+c＜0；③a﹣b+c=﹣9a；④若（﹣3，y1），（3，y2）是抛物线上两点，则y1＞y2，其中正确的序号是 ．

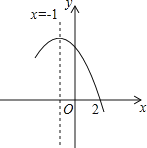
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，线段AB=12cm，延长AB到点C，使BC=AB，点D是BC中点，点E是AD中点．

    （1）根据题意，补全图形；

    （2）求DE的长；

    （3）若动点P从点A出发，以1cm/s的速度向点C运动，到达点C停止运动，点Q从点C出发，以2cm/s的速度向点A运动，到达点A停止运动，若运动时间为ts，当t为何值时，PQ=3cm？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在线段、平行四边形、矩形、等腰三角形、圆这几个图形中既是轴对称图形又是中心对称图形的个数是（ ）

    A．2个 B．3个 C．4个 D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个两位数，个位上的数字为x，十位上的数字为y，则这个两位数可表示为（ ）

    A．xy B．x+y C．10x+y D．x+10y

    查看答案和解析>>

    同步练习册答案