
【题目】如图,直线AB、CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
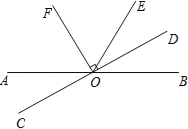
(1)若∠AOE=120°,求∠BOD的度数;
(2)写出图中所有与∠AOD互补的角: .
【答案】(1)30°;(2)∠AOC、∠BOD、∠DOE.
【解析】试题分析:(1)根据角平分线的性质可得∠AOF=![]() ∠AOE=60°,再由OF⊥CD,可得∠COF=90°,再根据角的和差关系可得∠AOC的度数,根据对顶角相等可得答案;
∠AOE=60°,再由OF⊥CD,可得∠COF=90°,再根据角的和差关系可得∠AOC的度数,根据对顶角相等可得答案;
(2)根据两个角的和为180°即为互补可得答案.
解:(1)∵OF平分∠AOE,∠AOE=120°,
∴∠AOF=![]() ∠AOE=60°.
∠AOE=60°.
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF﹣∠AOF=30°,
∵∠AOC和∠BOD是对顶角,
∴∠BOD=∠AOC=30°;
(2)与∠AOD互补的角有∠AOC、∠BOD、∠DOE,
故答案为:∠AOC、∠BOD、∠DOE.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ACB=90°,点D、E在AB上,将△ACD、△BCE分别沿CD、CE翻折,点A、B分别落在点A′、B′的位置,再将△A′CD、△B′CE分别沿A′C、B′C翻折,点D与点E恰好重合于点O,则∠A′OB′的度数是( )
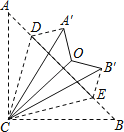
A.90° B.120° C.135° D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
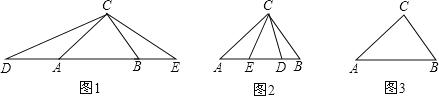
【题目】(1)如图(1),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在线段BA、AB的延长线上,且AD=AC,BE=BC,则∠DCE= ;
(2)如图(2),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在直线AB上,且AD=AC,BE=BC,则∠求DCE的度数(直接写出答案);
(4)如图(3),在△ABC中,AB=14,AC=15,BC=13,点D、E在直线AB上,且AD=AC,BE=BC.请根据题意把图形补画完整,并在图形的下方直接写出△DCE的面积.(如果有多种情况,图形不够用请自己画出,各种情况用一个图形单独表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接春节,某县准备用灯笼美化滨河路,许采用A、B两种不同造型的灯笼共600个.且A型灯笼的数量比B型灯笼的![]() 多15个.
多15个.
(1)求A、B两种灯笼各需多少个?
(2)已知A、B型灯笼的单价分别为40元、30元,则这次美化工程需多少费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织植树活动,已知在甲处植树的有14人,在乙处植树的有6人,现调70人去支援.
(1)若要使在甲处植树的人数与在乙处植树的人数相等,应调往甲处 人.
(2)若要使在甲处植树的人数是在乙处植树人数的2倍,问应调往甲、乙两处各多少人?
(3)通过适当的调配支援人数,使在甲处植树的人数恰好是在乙处植树人数的n倍(n是大于1的正整数,不包括1.)则符合条件的n的值共有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com