
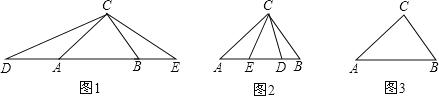
����Ŀ����1����ͼ��1��������ABC�У�AB��AC��BC����ACB=80������D��E�ֱ����߶�BA��AB���ӳ����ϣ���AD=AC��BE=BC������DCE= ��
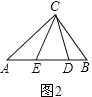
��2����ͼ��2��������ABC�У�AB��AC��BC����ACB=80������D��E�ֱ��ڱ�AB�ϣ���AD=AC��BE=BC������DCE�Ķ�����
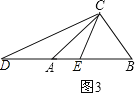
��3������ABC�У�AB��AC��BC����ACB=80������D��E�ֱ���ֱ��AB�ϣ���AD=AC��BE=BC��������DCE�Ķ�����ֱ��д���𰸣���
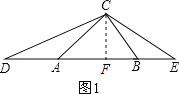
��4����ͼ��3��������ABC�У�AB=14��AC=15��BC=13����D��E��ֱ��AB�ϣ���AD=AC��BE=BC������������ͼ�β�������������ͼ�ε��·�ֱ��д����DCE�������������ж��������ͼ�β��������Լ����������������һ��ͼ�ε�����ʾ����
���𰸡���1��130�㣮��2��50������3��40������4��72��������
��������
�����������1�����ݵ��������ε����ʵõ���ACD=��D����BCE=��E���������ε��ڽǺ͵õ���CAB+��CBA=100�������������ε���ǵ����ʵõ���CDA+��BCE=![]() ����CAB+��CBA��=50�㣬���ɵõ����ۣ�
����CAB+��CBA��=50�㣬���ɵõ����ۣ�
��2�����������ε��ڽǺͺ���ǵ����ʼ��ɵõ����ۣ�
��3����D��E�ֱ���ֱ��AB�ϣ���ȥ��1����2��������������������������ͼ3���ɣ�1��֪����D=![]() CAB���ɣ�2��֪��CEB=
CAB���ɣ�2��֪��CEB=![]() ���з��̼�����ý����
���з��̼�����ý����
��4������ABC�У�AB=14��AC=15��BC=13����C��CF��AB��F�����ݹ��ɶ������AB���ϵĸ�CF=12��Ȼ����������ε������ʽ����ǿ��Ľ��ۣ�
�⣺��1����AD=AC��BE=BC��
���ACD=��D����BCE=��E��
�ߡ�ACB=80����
���CAB+��CBA=100����
���CDA+��BCE=![]() ����CAB+��CBA��=50�㣬
����CAB+��CBA��=50�㣬
���DCE=130����
�ʴ�Ϊ��130�㣮
��2���ߡ�ACB=80����
���A+��B=100����
��AD=AC��BE=BC��
���ACD=��ADC����BEC=��BCE��
���ADC=![]() ����BEC=
����BEC=![]() ��
��
���ADC+��BEC=180����![]() ����A+��B��=130�㣬
����A+��B��=130�㣬
���DCE=50����
��3����D��E�ֱ���ֱ��AB�ϣ���ȥ��1����2��������������������������ͼ3��
�ɣ�1��֪����D=![]() CAB���ɣ�2��֪��CEB=
CAB���ɣ�2��֪��CEB=![]() ��
��
���CEB=��D+��DCE��
��![]() =
=![]() CAB+��DCE��
CAB+��DCE��
���DCE=40����
��ͼ4��ͬ����DCE=40����
��4������ABC��AB=14��AC=15��BC=13��
��C��CF��AB��F��
��AC2��AF2=BC2��BF2����152��AF2=132����14��AF��2��
��ã�AF=9��
��CF=12��
����ͼ1��DE=AB+AC+BC=42��
��S��CDE=![]() ��42��12=252��
��42��12=252��
����ͼ2��DE=AC+BC��AB=14��
��S��CDE=![]() ��14��12=84��
��14��12=84��
����ͼ3��DE=AC+AB��BC=16��
��S��CDE=![]() ��16��12=96��
��16��12=96��
����ͼ4��DE=AB+BC��AC=12��
��S��CDE=![]() ��12��12=72��
��12��12=72��



 ������ϵ�д�
������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A����2��3����B��4��3����C����1����3����

��1�����C��x��ľ��룻
��2���ֱ�����ABC�����߳���
��3����P��y���ϣ�����ABP�����Ϊ6ʱ����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������O�ں��й����У����ֵ���A������ƫ��60��ķ����ϣ�ͬʱ��������ƫ��30�㡢����������ƫ��45�㣩�������ֱַ����˿���B�ͺ���C��
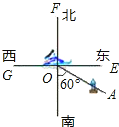
��1�����ձ�ʾ������λ�ķ������ֱ���ʾ����B�ͺ���C���������OB��OC����д��������
��2����ͼ����һ���洬D������AOD�IJ�����������ǵ�3����������ʾ�洬D���������OD�����洬D�ڻ���O�� ��д����λ�ǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OFƽ����AOE��OF��CD������ΪO��
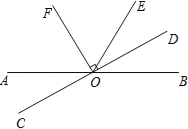
��1������AOE=120��������BOD�Ķ�����
��2��д��ͼ����������AOD�����Ľǣ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������ABT=45����AT=AB��
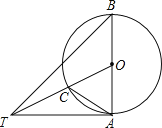
��1����֤��AT����O�����ߣ�
��2������OT����O�ڵ�C������AC����tan��TAC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016�괺���ڼ䣬���������á��ٶȡ������������������Ŷ�����������������֮��صĽ������ԼΪ45100000��������ÿ�ѧ��������ʾΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǹ涨������y=![]() ��a��b��k�dz�����k��ab�������غ�������a=b=0ʱ�����غ���y=
��a��b��k�dz�����k��ab�������غ�������a=b=0ʱ�����غ���y=![]() ���Ƿ���������y=
���Ƿ���������y=![]() ��k�dz�����k��0����
��k�dz�����k��0����
��1�����ijһ�������߳��ֱ���2��3�������Ƿֱ�����x��y�õ��¾��ε����Ϊ8����y��x֮��ĺ�������ʽ�����ж����Ƿ�Ϊ���غ�����
��2����ͼ����ƽ��ֱ������ϵxOy�У�����OABC�Ķ���A��C����ֱ�Ϊ��6��0������0��3������D��OA�е㣬����OB��CD����E�������غ���y=![]() ��ͼ����B��E��������غ����ı���ʽ��
��ͼ����B��E��������غ����ı���ʽ��
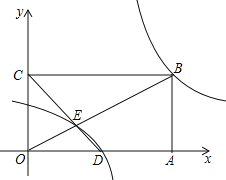
��3���ѷ���������y=![]() ��ͼ������ƽ��4����λ��������ƽ�� ����λ�Ϳɵõ���2���еõ������غ�����ͼ��
��ͼ������ƽ��4����λ��������ƽ�� ����λ�Ϳɵõ���2���еõ������غ�����ͼ��
��4���ڣ�2���������£����߶�BE�е�M��һ��ֱ��l��������غ���ͼ����P��Q���㣨P��Q�Ҳࣩ�������B��E��P��QΪ������ɵ��ı������Ϊ16����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB=12cm���ӳ�AB����C��ʹBC=![]() AB����D��BC�е㣬��E��AD�е㣮
AB����D��BC�е㣬��E��AD�е㣮
![]()
��1���������⣬��ȫͼ�Σ�
��2����DE�ij���
��3��������P�ӵ�A��������1cm/s���ٶ����C�˶��������Cֹͣ�˶�����Q�ӵ�C��������2cm/s���ٶ����A�˶��������Aֹͣ�˶������˶�ʱ��Ϊts����tΪ��ֵʱ��PQ=3cm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com