
【题目】如图,AB是⊙O的直径,∠ABT=45°,AT=AB.
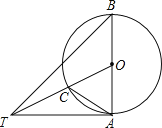
(1)求证:AT是⊙O的切线;
(2)连接OT交⊙O于点C,连接AC,求tan∠TAC.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)根据等腰三角形的性质求得∠TAB=90°,得出TA⊥AB,从而证得AT是⊙O的切线;
(2)作CD⊥AT于D,设OA=x,则AT=2x,根据勾股定理得出OT=![]() x,TC=(
x,TC=(![]() ﹣1)x,由CD⊥AT,TA⊥AB得出CD∥AB,根据平行线分线段成比例定理得出
﹣1)x,由CD⊥AT,TA⊥AB得出CD∥AB,根据平行线分线段成比例定理得出![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,从而求得CD=(1﹣
,从而求得CD=(1﹣![]() )x,AD=2x﹣2(1﹣
)x,AD=2x﹣2(1﹣![]() )x=
)x=![]() x,然后解正切函数即可求得.
x,然后解正切函数即可求得.
解:(1)∵∠ABT=45°,AT=AB.
∴∠TAB=90°,
∴TA⊥AB,
∴AT是⊙O的切线;
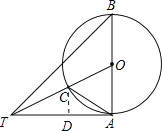
(2)作CD⊥AT于D,
∵TA⊥AB,TA=AB=2OA,
设OA=x,则AT=2x,
∴OT=![]() x,
x,
∴TC=(![]() ﹣1)x,
﹣1)x,
∵CD⊥AT,TA⊥AB
∴CD∥AB,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴CD=(1﹣![]() )x,TD=2(1﹣
)x,TD=2(1﹣![]() )x,
)x,
∴AD=2x﹣2(1﹣![]() )x=
)x=![]() x,
x,
∴tan∠TAC=![]() =
=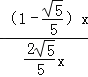 =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,﹣2).
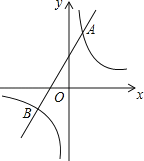
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用科学记数法表示0.00001032,下列正确的是( )
A. 0.1032×10-4 B. 1.032×103 C. 10.32×10-6 D. 1.032×10-5
查看答案和解析>>
科目:初中数学 来源: 题型:
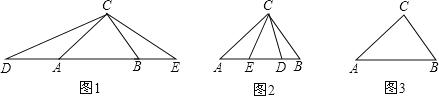
【题目】(1)如图(1),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在线段BA、AB的延长线上,且AD=AC,BE=BC,则∠DCE= ;
(2)如图(2),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在直线AB上,且AD=AC,BE=BC,则∠求DCE的度数(直接写出答案);
(4)如图(3),在△ABC中,AB=14,AC=15,BC=13,点D、E在直线AB上,且AD=AC,BE=BC.请根据题意把图形补画完整,并在图形的下方直接写出△DCE的面积.(如果有多种情况,图形不够用请自己画出,各种情况用一个图形单独表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC,则y关于x函数的图象大致为( )

A.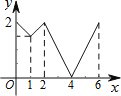 B.
B.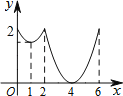
C.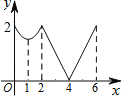 D.
D.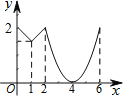
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的方格纸中,有一个以格点为顶点的△ABC.
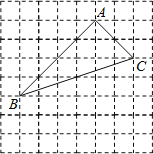
(1)试根据三角形三边关系,判断△ABC的形状;
(2)在方格纸中利用直尺分别画出AB、BC的垂直平分线,交点为O.观察点O的位置,你能得出怎样的结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家莫伦在1925年发现了世界上第一个完美长方形.如图是一个完美长方形,它恰能被分割成10个大小不同的正方形,其中标注番号1的正方形边长为5,则这个完美长方形的面积为 .
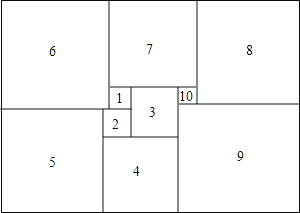
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com