
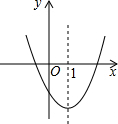 如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,

 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
 太原市公共自行车项目是为了缓解交通拥堵、减少环境污染和方便市民出行的民生工程重点项目之一,截止2014年12月,累计租骑公共自行车总量已达到2.217亿车次,这个数据用科学记数法表示为
太原市公共自行车项目是为了缓解交通拥堵、减少环境污染和方便市民出行的民生工程重点项目之一,截止2014年12月,累计租骑公共自行车总量已达到2.217亿车次,这个数据用科学记数法表示为查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
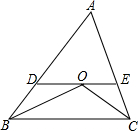 如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.
如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、必然事件 | B、随机事件 |
| C、不可能事件 | D、以上都不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com