
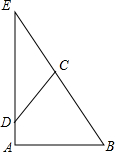
 如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是0<CD≤5.
如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是0<CD≤5. 科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
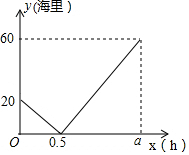 在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.
在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com