
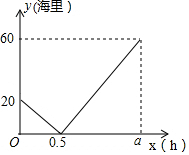
 在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.
在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(时)后,与B港的距离为y(海里),y与x之间的函数图象如图所示.分析 (1)把A到B、B到C间的距离相加即可得到A、C两个港口间的距离,再求出海巡船的速度,然后根据时间=路程÷速度,计算即可求出a值;
(2)分0<x≤0.5和0.5<x≤1.7两段,利用待定系数法求一次函数解析式求解即可;
(3)根据函数解析式求出距离为8km时的时间,然后相减即可得解.
解答 解:(1)由图可知,A、B港口间的距离为20,B、C港口间的距离为60,
所以,A、C港口间的距离为:20+60=80km,
海巡船的速度为:20÷0.5=40km/h,
∴a=80÷40=2h,
故答案为:80,2h;
(2)当0<x≤0.5时,设y与x的函数关系式为:y=kx+b,
∵函数图象经过点(0,20),(0.5,0)
∴$\left\{\begin{array}{l}{b=20}\\{0.5k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-40}\\{b=20}\end{array}\right.$.
所以,y=-0x+20;
当0.5<x≤1.7时,设y与x的函数关系式为:y=mx+n,
∵函数图象经过点(0.5,0),(2,60),
∴$\left\{\begin{array}{l}{0.5m+n=0}\\{2m+n=60}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=40}\\{n=-20}\end{array}\right.$.
所以,y=40x-20,
(3)当0≤x≤0.5,y=8时,-40x+20=8,
解得x=0.,
当0.5<x≤2,y=8时,40x-20=8,
解得x=0.7,
∴0.7-0.3=0.4
答:该海巡船能接受到该信号的时间为:0.4h.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,已知函数值求自变量,比较简单,理解题目信息是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
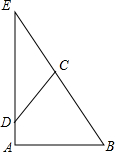 如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是0<CD≤5.
如图,已知Rt△ABE中∠A=90°,∠B=60°,BE=10,D是线段AE上的一动点,过D作CD交BE于C,并使得∠CDE=30°,则CD长度的取值范围是0<CD≤5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
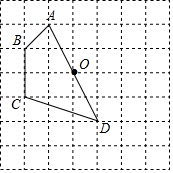 如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转90°,试解决下列问题:
如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转90°,试解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com