练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】分别用a、b表示任一有理数，如果|a|=7，|b|=5，试求a-b的值.

    【答案】±2或±12．

    【解析】

    根据绝对值的性质求出a、b的值，然后分情况讨论求解．

    ∵|a|=7，|b|=5，

    ∴a=±7，b=±5，

    因此有四种可能：

    ①a=7，b=5时，a-b=7-5=2；

    ②a=7，b=-5时，a-b=7-（-5）=7+5=12；

    ③a=-7，b=5时，a-b=-7-5=-12；

    ④a=-7，b=-5时，a-b=-7-（-5）=-7+5=-2，

    综上所述，a-b的值是±2或±12．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

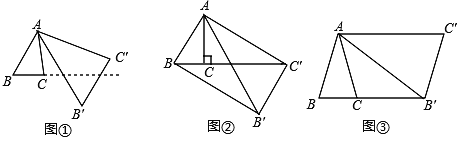
    【题目】将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′ ，如图①所示，∠BAB′ ＝θ， ，我们将这种变换记为[θ，n] ．

    （1）如图①，对△ABC作变换[60°，]得到△AB′C′ ，则:= ；直线BC与直线B′C′所夹的锐角为 度；

    （2）如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、在同一直线上，且四边形ABB′C′为矩形，求θ和n的值；

    （3）如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

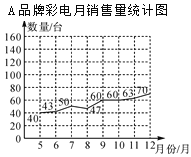
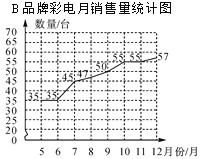
    【题目】某家电商场A、B两种品牌彩电2016年5～12月销售量统计如图．

    (1)有人认为B品牌彩电销售量比A品牌彩电销售量增长快．你同意这种观点吗？

    (2)根据统计图进行比较、判断时要注意些什么？

    (3)如果你是商场经理，从上面的统计图中你能得到哪些信息？对你有什么帮助？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知直线y=2x﹣5经过点A（a，1﹣a），则A点落在第_____象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知a=29，b=-36，c=-216，则(-a)+b-(-c)=_______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    我们知道的几何意义是在数轴上数对应的点与原点的距离；即；这个结论可以推广为表示在数轴上数， 对应点之间的距离．绝对值的几何意义在解题中有着广泛的应用：

    例1：解方程．

    容易得出，在数轴上与原点距离为4的点对应的数为±4，即该方程的±4；

    例2：解方程．

    由绝对值的几何意义可知，该方程表示求在数轴上与-1和2的距离之和为5的点对应的的值．在数轴上，-1和2的距离为3，满足方程的对应的点在2的右边或在-1的左边．若对应的

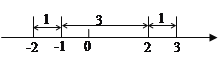
    点在2的右边，如图可以看出；同理，若对应点在-1的左边，可得．所以原方程的解是或．

    例3：解不等式．

    在数轴上找出的解，即到1的距离为3的点对应的数为-2，4，如图，在-2的左边或在4的右边的值就满足，所以的解为或．

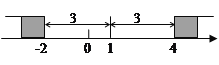
    参考阅读材料，解答下列问题：

    （1）方程的解为　 　；

    （2）方程的解为　 ；

    （3）若，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】多项式8x2﹣3x+5与多项式3x3+2mx2﹣5x+7相加后，不含二次项，则常数m的值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

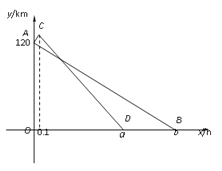
    【题目】（本题满分10分）从M地到N地有一条普通公路，总路程为120km；有一条高速公路，总路程为126km．甲车和乙车同时从M地开往N地，甲车全程走普通公路，乙车先行驶了另一段普通公路，然后再上高速公路．假设两车在普通公路和高速公路上分别保持匀速行驶，其中在普通公路上的行车速度为60km/h，在高速公路上的行车速度为100km/h．设两车出发x h时，距N地的路程为y km，图中的线段AB与折线ACD分别表示甲车与乙车的y与x之间的函数关系．

    （1）填空：a＝ ，b＝ ；

    （2）求线段AB、CD所表示的y与x之间的函数关系式；

    （3）两车在何时间段内离N地的路程之差达到或超过30km？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

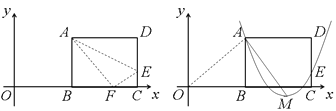
    【题目】如图（1），矩形ABCD的一边BC在直角坐标系中x轴上，折叠边AD,使点D落在x轴上点F处，折痕为AE，已知AB=8，AD=10，并设点B坐标为（m,0），其中m＞0.

    （1）求点E、F的坐标（用含m的式子表示）；（5分）

    （2）连接OA，若△OAF是等腰三角形，求m的值；（4分）

    （3）如图（2），设抛物线y=a(x－m－6)2+h经过A、E两点，其顶点为M，连接AM，若∠OAM=90°，求a、h、m的值. （5分）

    查看答案和解析>>

    同步练习册答案