
����Ŀ����ͼ�������� ![]() ��ͼ�����C��0��1��������ΪQ��2��3��,��D��x���������ϣ��߶�OD=OC.
��ͼ�����C��0��1��������ΪQ��2��3��,��D��x���������ϣ��߶�OD=OC.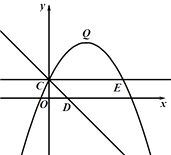
��1���������ߵĽ���ʽ��
��2�����������Ƿ���ڵ�M��ʹ�á�CDM����CDΪֱ�DZߵ�ֱ�������Σ������ڣ������M������ꣻ�������ڣ���˵�����ɣ�
��3����ֱ��CD�Ƶ�C��ʱ�뷽����ת45������ֱ�����������ཻ����һ��E������QE.����P���߶�QE�ϵĶ��㣬��F���߶�OD�ϵĶ��㣬�ʣ���P���F����ƶ������У���PCF���ܳ��Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵������.
���𰸡�
��1���⣺�������ߵĽ���ʽΪ ![]() ��
��
��C��0��1������ã� ![]() ��
��
���: ![]() ,
,
�������ߵĽ���ʽΪ�� ![]() ��
�� ![]()
��2����: ����ͼ1������CΪֱ�Ƕ���ʱ��
�ߵ�C������Ϊ��0��1����
��OD=OC=1��
���D��������1��0����
��ֱ��CDΪ ![]() ����
���� ![]() �����
����� ![]() ��
��
��ֱ��CD�Ľ���ʽΪ�� ![]() ��
��
�ߴ�ʱCM��CD��
��CM�Ľ���ʽΪ�� ![]() ��
��
�ɣ� 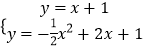 ����ã�
����ã� ![]() ��
�� ![]() ��
��
�ߵ㣨0��1�����C�غϣ�
���M������Ϊ��2��3������ʱ��M���Q�غϣ�
����ͼ�ڣ���DΪֱ�Ƕ���ʱ���ɢٿɵ�ֱ��DM�Ľ���ʽΪ ![]() ��
��
�ɣ�  ,��ã�
,��ã� ![]() ��
�� ![]() ��
��
���͵�����ΪΪ ![]() ��
�� ![]() ��
��
������������������ģ������㣬�ֱ���(2 , 3 )�� ![]() ��
�� ![]() .
.
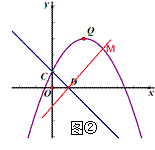
��3���⣺���ڣ���ͼ����ʾ������C����ֱ��QE�ĶԳƵ�C�䣬����C����x��ĶԳƵ�C�壬����C��C�壬��OD�ڵ�F����QE�ڵ�P�����PCF��Ϊ����������ܳ���С�������Σ�����ԳƵ����ʿ�֪����PCF���ܳ������߶�C��C��ij��ȣ�
���ͼ����ʾ������C��E��
�ɣ�2����֪��QC��CD�� ������ɵã�QC=QE��
�ߡ�DCE=45�㣬
���QCE=45��=��QEC��
���QCE�ǵ���ֱ�������Σ�
��C��C�����ֱ��QE�Գƣ�
���QC��EΪ����ֱ�������Σ�
���CEC��Ϊ����ֱ�������Σ�
���������� ![]() ����
���� ![]() ���
��� ![]() ��
��
���E��������4��1����
��CE=4=C��E��
���C���������4��5����
��C��C�����x��Գƣ�
���C���������0����1����
��OC��=1��
����C����C��N��y���ڵ�N����NC��=CE=4��NC��=4+1+1=6��
��Rt��C��NC���У��ɹ��ɶ����ã�C��C��= ![]() ��
��
������������P���F���ƶ������У���PCF���ܳ�������Сֵ����СֵΪ ![]() ��
��
����������1������ʽ����Ϊ����ʽ���ٰ�C��0��1���������ʽ���ɣ���2����CDΪֱ�DZߵ�ֱ�������η�Ϊ���࣬�ֱ���C��DΪֱ�Ƕ��㣬�ɹ�C��D�ֱ���CD�Ĵ��ߣ����������ཻ������ֱ�ߺ������߽���ʽ��ɷ����飬�����M���ꣻ��3�������öԳƷ�����C���ڶ�ֱ��QE�ĶԳƵ�C'������y��ԳƵ�ΪC",�ѡ�PCF���ܳ�ת��ΪFC"+FP+PC',��C"��F��P��C'�ĵ㹲��ʱ���ܳ���С.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ����ABCD�У���E��F��AD��BC���е㣬����BE��DF��
��1����֤��BE��DF��
��2����BEƽ�֡�ABC�ҽ���AD�ڵ�E��AB=6cm��BC=10cm�������߶�DE�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���֪��A��0��10������P��m��10��������AP��OP������AOP��ֱ��OP���۵õ���EOP����A�Ķ�Ӧ��Ϊ��E��������E��x��ľ��벻����6����m��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=26cm��BC=20cm��D��AB���е㣬��D��DE��AC��E����DE�ij�Ϊ____��
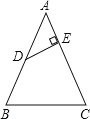
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1���Ҿ�A��1��0����B��0����3�����㣮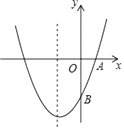
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ���x=��1�ϣ��Ƿ���ڵ�M��ʹ������A�ľ����뵽��B�ľ���֮����С��������������M�����꣬�����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90����D��E�ֱ�ΪAB��AC���ϵ��е㣬����DE������ADE�Ƶ�E��ת180���õ���CFE������AF��AC��

��1����֤���ı���ADCF�����Σ�
��2����BC=8��AC=6�����ı���ABCF���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ֽ����Ǽ����߳��ֱ�Ϊ20cm��50cm��60cm����Ҫ����һ���������Ƶĸֽ����Ǽܣ���ֻ�г�Ϊ30cm��50cm�������ֽҪ�������е�һ��Ϊһ�ߣ�����һ����������(����������)��Ϊ�����ߣ���ͬ�Ľط���( ).
A. һ�� B. ���� C. ���� D. ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������һ��ͼ�Σ�ͨ����ͬ�ķ�������ͼ�ε�������Եõ�һ����ѧ��ʽ��
���磺��ͼ1�ɵõ�(a+b)=a+2ab+b��
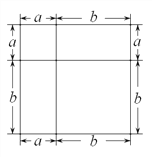
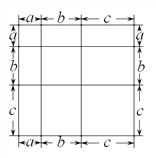
ͼ1 ͼ2 ͼ3
��1��д����ͼ2����ʾ����ѧ��ʽ��_____________________��д����ͼ3����ʾ����ѧ��ʽ��_____________________��
��2�������������ۣ�����������⣺��֪a+b+c=11��bc+ac+ab=38����a+b+c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���Ӧ�ã�
�Ķ�1��a��bΪʵ������a��0��b��0����Ϊ ![]() ������
������ ![]() ���Ӷ�
���Ӷ� ![]() ����a��bʱȡ�Ⱥţ���
����a��bʱȡ�Ⱥţ���
�Ķ�2������ ![]() ������m��0��x��0�������Ķ�1���ۿ�֪��
������m��0��x��0�������Ķ�1���ۿ�֪�� ![]()
![]() �����Ե�
�����Ե� ![]() ��
�� ![]() ʱ������
ʱ������ ![]() ����СֵΪ
����СֵΪ ![]() ��
��
�Ķ������������ݣ�����������⣺
��1������1����֪һ�����ε����Ϊ4������һ�߳�Ϊx������һ�߳�Ϊ ![]() ���ܳ�Ϊ
���ܳ�Ϊ ![]() ����x��ʱ���ܳ�����СֵΪ ��
����x��ʱ���ܳ�����СֵΪ ��
��2������2����֪����y1��x��1��x����1���뺯��y2��x2��2x��17��x����1������x��ʱ�� ![]() ����СֵΪ ��
����СֵΪ ��
��3������3��ij���ѧϰÿ���֧���ܷ��ð��������������֣�һ�ǽ�ְ������6400Ԫ������ѧ�������ÿ��10Ԫ�������������ã����У�����������ѧ��������ƽ�������ȣ�����ϵ��Ϊ0.01����ѧУѧ������Ϊ����ʱ����Уÿ������Ͷ����ͣ���ͷ����Ƕ���Ԫ��������Ͷ�룽֧���ܷ��á�ѧ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com