
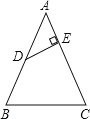
【题目】如图,在△ABC中,AB=AC=26cm,BC=20cm,D是AB的中点,过D作DE⊥AC于E,则DE的长为____.
【答案】![]() cm.
cm.
【解析】
过A作BC的垂线,由勾股定理易求得此垂线的长,即可求出△ABC的面积;连接CD,由于AD=BD,则△ADC、△BCD等底同高,它们的面积相等,由此可得到△ACD的面积;进而可根据△ACD的面积求出DE的长.
解:过A作AF⊥BC于F,连接CD;
△ABC中,AB=AC=26cm,AF⊥BC,则BF=FC![]() BC=10(cm);
BC=10(cm);
Rt△ABF中,AB=26cm,BF=10cm;
由勾股定理,得AF![]() 24(cm);
24(cm);
∴S△ABC![]() BCAF=240(cm2).
BCAF=240(cm2).
∵AD=BD,
∴S△ADC=S△BCD![]() S△ABC=120(cm2).
S△ABC=120(cm2).
∵S△ADC![]() ACDE=120(cm2),
ACDE=120(cm2),
则DE![]() (cm).
(cm).
故答案为:![]() cm.
cm.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:
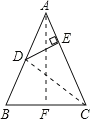
【题目】如图,在四边形![]() 中,
中,![]() ,点
,点![]() 分别从点
分别从点![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动,点
运动,点![]() 以
以![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动设运动时间为
运动设运动时间为![]() .当
.当![]() __________.时,
__________.时,![]() 为平行四边形的一边.
为平行四边形的一边.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,AB=BC,AB>CD,AE⊥BD于E交BC于F.

(1)若AB=2CD;
①求证:BC=2BF;
②连CE,若DE=6,CE=![]() ,求EF的长;
,求EF的长;
(2)若AB=6,则CE的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
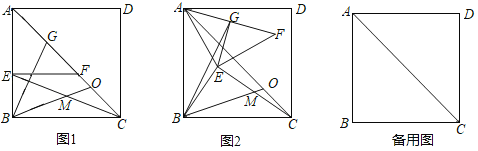
【题目】在正方形ABCD中,AB=6,E为直线AB上一点,EF⊥AB交对角线AC于F,点G为AF中点,连接CE,点M为CE中点,连接BM并延长交直线AC于点O.
(1)如图1,E在边AB上时,![]() = ,∠GBM= ;
= ,∠GBM= ;
(2)将(1)中△AEF绕A逆时针旋转任意一锐角,其他条件不变,如图2,(1)中结论是否任然成立?请加以证明.
(3)若BE=2,则CO长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
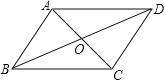
A.AB=DC,AD=BCB.AB∥DC,AD∥BC
C.AB∥DC,AD=BCD.OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作: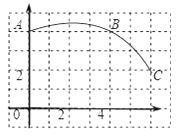
(1)请在图中确定该圆弧所在圆心D点的位置,求出D点坐标
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.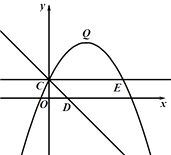
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得△CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家旅行社为了吸引更多的顾客,分别提出了赴某地旅游的团体优惠方法,甲旅行社的优惠方法是:买4张全票,其余人按半价优惠;乙旅行社的优惠方法是:一律按7折优惠,已知两家旅行社的原价均为每人100元;那么随着团体人数的变化,哪家旅行社的收费更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
(1)你认为图2中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法求图2中阴影部分的面积.
方法1 ;方法2 ;
(3)仔细观察图2,写出![]() 三个代数式之间的等量关系.
三个代数式之间的等量关系.
(4)若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com