
【题目】在正方形ABCD中,AB=6,E为直线AB上一点,EF⊥AB交对角线AC于F,点G为AF中点,连接CE,点M为CE中点,连接BM并延长交直线AC于点O.
(1)如图1,E在边AB上时,![]() = ,∠GBM= ;
= ,∠GBM= ;
(2)将(1)中△AEF绕A逆时针旋转任意一锐角,其他条件不变,如图2,(1)中结论是否任然成立?请加以证明.
(3)若BE=2,则CO长为 .
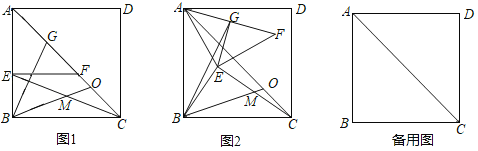
【答案】(1)![]() ,45°;(2)成立,理由见解析;(3)
,45°;(2)成立,理由见解析;(3)![]() 或3
或3![]() .
.
【解析】
(1)连结EG、GM.想办法证明△GBM是等腰直角三角形即可解决问题.
(2)成立.延长GM到H,使得MH=GM,连接BH,HC,延长HC交AF的延长线于I,设AI交CD于J.利用全等三角形的性质证明△GBM是等腰直角三角形即可解决问题.
(3)分两种情形①点E在线段AB上.②点E在AB的延长线上,分别求解即可解决问题.
解:(1)连结EG、GM.
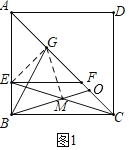
∵四边形ABCD是正方形,
∴∠ABC=90°,∠CAB=∠ACB=45°,
∵EF⊥AB,
∴∠AEF=90°,
∴∠EAF=∠EFA=45°,
∵AG=GF,
∴EG⊥AF,
∴∠EGC=90°
∵EM=MC,
∴GM=BM=![]() CE,
CE,
∴∠MCG=∠MGC,∠MBC=∠MCB,
∴∠BMG=∠BME+∠GME=2∠BMC+2∠GCM=2∠ACB=90°.
故△GMB为等腰直角三角形.
∴![]() .
.
故答案为![]() ,45°.
,45°.
(2)成立.
理由:延长GM到H,使得MH=GM,连接BH,HC,延长HC交AF的延长线于I,设AI交CD于J.
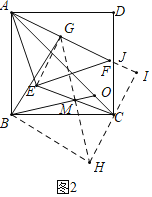
∵EM=MC,GM=MH,∠EMG=∠HMC,
∴△EMG≌△CMH(SAS),
∴EG=CH,∠EGM=∠MHC,
∴EC∥CH,
∴∠AGE=∠AIH=90°,
∵AG=EG,
∴AG=CH,
∵∠D=∠I=90°,∠AJD=∠CJI,
∴∠ICD=∠IAD,
∵∠BAG+∠IAD=90°,∠BCH+∠ICF=90°
∴∠BCH=∠BAG,
∵BA=BC
∴△BAG≌△BCH(SAS),
∴BG=DH,∠ABG=∠CBH,
∴∠∠GBH=∠ABC=90°
故△GBH是等腰直角三角形,
∴![]() ,∠GBM=45°.
,∠GBM=45°.
(3)当E在B上方时,如图3﹣1中,延长BO交CD于T.
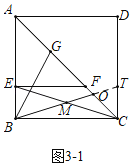
∴BE∥CT,
∴∠MEB=∠MCT,
∵∠EMB=∠CMT,EM=CM,
∴△EMB≌△CMT(ASA),
∴BE=CT=2,
∵CT∥AB,
∴![]() ,
,
∵AC=6![]() ,
,
∴OC=![]() ×6
×6![]()
∴CO=![]()
当E在B下方时同法可得CO=3![]() .
.
综上所述,OC的长为![]() 或3
或3![]() .
.
故答案为![]() 或3
或3![]() .
.


科目:初中数学 来源: 题型:
【题目】用如图所示的卡片拼成一个长为(2a+3b),宽为(a+b)的长方形,则需要(1)型卡片、(2)型卡片和(3)型卡片的张数分别是( )

A. 2,5,3B. 2,3,5C. 3,5,2D. 3,2,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)(x3)2.(﹣x4)3
(2)(![]() x5y4﹣
x5y4﹣![]() x4y3)
x4y3)![]() x3y3
x3y3
(3)(2a+1)2﹣(2a+1)(2a﹣1)
(4)102+![]() ×(π﹣3.14)0﹣|﹣302|
×(π﹣3.14)0﹣|﹣302|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知点A(0,10),点P(m,10),连接AP、OP,将△AOP沿直线OP翻折得到△EOP(点A的对应点为点E).若点E到x轴的距离不大于6,则m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
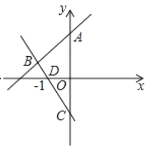
【题目】如图,在平面直角坐标系中,直线y=x+4交y轴于点A,与直线BC相交于点B(-2,m),直线BC与y轴交于点C(0,-2),与x轴交于点D.
(1)求点B坐标;
(2)求△ABC的面积
(3)过点A作BC的平行线交x轴于点E,求点E的坐标;
(4)在(3)的条件下,点p是直线AB上一动点且在x轴上方,Q为直角坐标平面内一点,如果以点D、E、P、Q为顶点的平行四边形的面积等于△ABC面积请求出点P的坐标.并直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB

(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com