
【题目】 如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB

(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据平行四边形的对边互相平行可得AD∥BC,再根据两直线平行,内错角相等可得∠AEB=∠EAD,根据等边对等角可得∠ABE=∠AEB,即可得证.
(2)根据两直线平行,内错角相等可得∠ADB=∠DBE,然后求出∠ABD=∠ADB,再根据等角对等边求出AB=AD,然后利用邻边相等的平行四边形是菱形证明即可.
证明:(1)∵在平行四边形ABCD中,AD∥BC,
∴∠AEB=∠EAD.
∵AE=AB,
∴∠ABE=∠AEB.
∴∠ABE=∠EAD.
(2)∵AD∥BC,
∴∠ADB=∠DBE.
∵∠ABE=∠AEB,∠AEB=2∠ADB,
∴∠ABE=2∠ADB.
∴∠ABD=∠ABE-∠DBE=2∠ADB-∠ADB=∠ADB.
∴AB=AD.
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
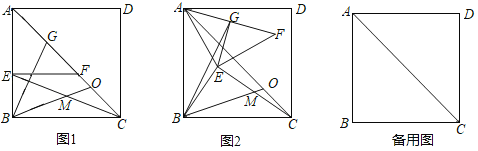
【题目】在正方形ABCD中,AB=6,E为直线AB上一点,EF⊥AB交对角线AC于F,点G为AF中点,连接CE,点M为CE中点,连接BM并延长交直线AC于点O.
(1)如图1,E在边AB上时,![]() = ,∠GBM= ;
= ,∠GBM= ;
(2)将(1)中△AEF绕A逆时针旋转任意一锐角,其他条件不变,如图2,(1)中结论是否任然成立?请加以证明.
(3)若BE=2,则CO长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家旅行社为了吸引更多的顾客,分别提出了赴某地旅游的团体优惠方法,甲旅行社的优惠方法是:买4张全票,其余人按半价优惠;乙旅行社的优惠方法是:一律按7折优惠,已知两家旅行社的原价均为每人100元;那么随着团体人数的变化,哪家旅行社的收费更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交函数
轴的直线,交函数![]() 的图象于点
的图象于点![]() .
.
①当![]() 时,判断线段
时,判断线段![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
(3)设![]() ,
,![]() 是这个反比例函数图象上任意不重合的两点,
是这个反比例函数图象上任意不重合的两点,![]() ,
,![]() ,试判断
,试判断![]() ,
,![]() 的大小,并说明理由.
的大小,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与拓展应用,
已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;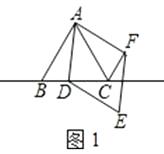
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;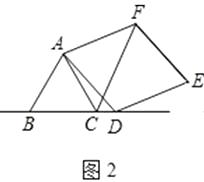
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.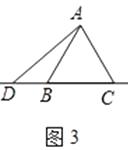
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1 , 它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,它交x轴于A2;将C2绕A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C7 , 若点P(13,m)在第7段抛物线C7上,则m= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
(1)你认为图2中的阴影部分的正方形的边长等于 .
(2)请用两种不同的方法求图2中阴影部分的面积.
方法1 ;方法2 ;
(3)仔细观察图2,写出![]() 三个代数式之间的等量关系.
三个代数式之间的等量关系.
(4)若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0)、A(0,6)、B(4,6)、C(4,4)、D(6,4),E(6,0),若直线L经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线L的函数表达式是 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com