
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作: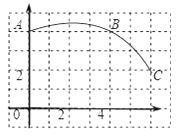
(1)请在图中确定该圆弧所在圆心D点的位置,求出D点坐标
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】某县教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,![]() 级:对学习很感兴趣;
级:对学习很感兴趣;![]() 级:对学习较感兴趣;
级:对学习较感兴趣;![]() 级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:

(1)此次抽样调查中,共调查了多少名学生;
(2)将图①补充完整;
(3)求出图②中![]() 级所占的圆心角的度数;
级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该县近12000名八年级学生中大约有多少名学生学习态度达标(达标包括![]() 级和
级和![]() 级)?
级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)(x3)2.(﹣x4)3
(2)(![]() x5y4﹣
x5y4﹣![]() x4y3)
x4y3)![]() x3y3
x3y3
(3)(2a+1)2﹣(2a+1)(2a﹣1)
(4)102+![]() ×(π﹣3.14)0﹣|﹣302|
×(π﹣3.14)0﹣|﹣302|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+4交y轴于点A,与直线BC相交于点B(-2,m),直线BC与y轴交于点C(0,-2),与x轴交于点D.
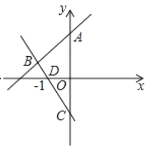
(1)求点B坐标;
(2)求△ABC的面积
(3)过点A作BC的平行线交x轴于点E,求点E的坐标;
(4)在(3)的条件下,点p是直线AB上一动点且在x轴上方,Q为直角坐标平面内一点,如果以点D、E、P、Q为顶点的平行四边形的面积等于△ABC面积请求出点P的坐标.并直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种成本为每件30元的商品,销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=-10x+600,商场销售该商品每月获得利润为w(元).
(1)求w与x之间的函数关系式;
(2)如果商场销售该商品每月想要获得2000元的利润,那么每月成本至少多少元?
(3)为了保护环境,政府部门要求用更加环保的新产品替代该商品,商场销售新产品,每月的销量与销售价格之间的关系与原产品的销售情况相同,新产品的成本每件32元,若新产品每月的销售量不低于200件时,政府部门给予每件4元的补贴,试求定价多少元时,每月销售新产品的利润最大?求出最大的利润。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要测量河宽,可在两岸找到相对的两点A、B,先从B出发与AB成90°方向向前走50米,到C处立一标杆,然后方向不变继续朝前走10米到D处,在D处转90°,沿DE方向走到E处,若A、C、E三点恰好在同一直线上,且DE=17米,你能根据题目提供的数据和图形求出河宽吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的斜边![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 与原点重合,点
与原点重合,点![]() 的坐标是
的坐标是![]() ,且
,且![]() ,若将
,若将![]() 绕着点
绕着点![]() 旋转后30°,点
旋转后30°,点![]() 和
和![]() 点分别落在点
点分别落在点![]() 和点
和点![]() 处,那么直线
处,那么直线![]() 的解析式是__________.
的解析式是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com