【题目】（2017浙江省嘉兴市，第20题，8分）如图，一次函数
（
）与反比例函数
（
）的图象交于点A（﹣1，2），B（m，﹣1）．
（1）求这两个函数的表达式；
（2）在x轴上是否存在点P（n，0）（n＞0），使△ABP为等腰三角形？若存在，求n的值；若不存在，说明理由．
【答案】（1）
，y=﹣x+1；（2）n=
或
．
【解析】试题分析：（1）利用待定系数法即可解决问题；
（2）分三种情形讨论：①PA=PB，② AP=AB，③BP=BA．分别解方程即可解决问题；
试题解析：（1）把A（﹣1，2）代入
，得到k2=﹣2，∴反比例函数的解析式为
．
∵B（m，﹣1）在上，∴m=2，由题意得：
，解得：
，∴一次函数的解析式为y=﹣x+1．
（2）∵A（﹣1，2），B（2，﹣1），∴AB=
，分三种情况讨论：
①当PA=PB时，（n+1）2+4=（n﹣2）2+1，∴n=0，∵n＞0，∴n=0不合题意舍弃．
②当AP=AB时，22+（n+1）2=（）2，∵n＞0，∴n=﹣1+
．
③当BP=BA时，12+（n﹣2）2=（）2，∵n＞0，∴n=2+
．
综上所述，n=
或．
科目：初中数学 来源： 题型：
【题目】如图，要得到AB∥CD，只需要添加一个条件，这个条件不可以是（ ）
A. ∠1＝∠3 B. ∠B＋∠BCD＝180°
C. ∠2＝∠4 D. ∠D＋∠BAD＝180°
查看答案和解析>>
科目：初中数学 来源： 题型：
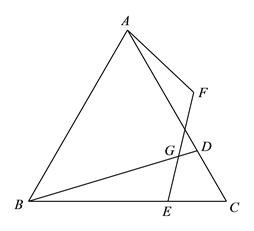
【题目】如图，在等边
中， 
分别是边
上的点，且
,
，点
与点
关于
对称，连接
，
交于
.
（1）连接
，则之间的数量关系是 ；
（2）若
，求
的大小（用
的式子表示）
（2）用等式表示线段
和
之间的数量关系，并证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
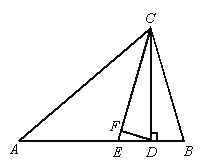
【题目】如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F，
(1)试说明CD是△CBE的角平分线；
(2)和∠B相等的角是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（题文）如图，在矩形ABCD中，点E是AD上的一个动点，连接BE，作点A关于BE的对称点F，且点F落在矩形ABCD的内部，连结AF，BF，EF，过点F作GF⊥AF交AD于点G，设 
=n.
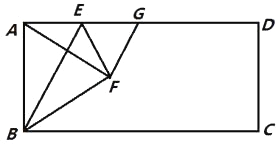
（1）求证：AE=GE；
（2）当点F落在AC上时，用含n的代数式表示
的值；
（3）若AD=4AB，且以点F，C，G为顶点的三角形是直角三角形，求n的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合)DE∥AB交AC于点F,CE∥AM,连结AE.
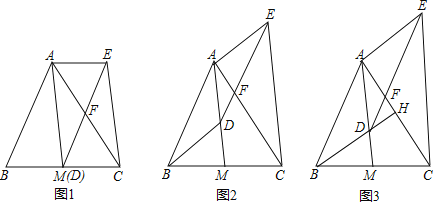
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM
①求∠CAM的度数;
②当FH=
, DM=4时,求DH的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
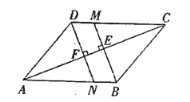
【题目】（1）如图，在平行四边形
中，过点
作
于点
，交
于点
，过点
作
于点
，交
于点
.
①求证：四边形
是平行四边形；
②已知
，求
的长.
（2）已知函数
.
①若函数图象经过原点，求
的值
②若这个函数是一次函数，且
随着
的增大而减小，求的取值范围
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】长江中下游地区特大旱情发生后，全国人民抗旱救灾，众志成城．市政府筹集了抗旱必需物资120吨打算运往灾区，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如下表所示：（假设每辆车均满载）
车型 | 甲 | 乙 | 丙 |
汽车运载量（吨/辆） | 5 | 8 | 10 |
汽车运费（元/辆） | 400 | 500 | 600 |
（1）若全部物资都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？
（2）为了节省运费，温州市政府打算用甲、乙、丙三种车型同时参与运送，已知它们的总辆数为14辆，你能分别求出三种车型的辆数吗？此时的运费又是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，0是坐标原点，点A坐标为(2， 0)，点B坐标为(0， b) (b>0)， 点P是直线AB上位于第二象限内的一个动点，过点P作PC垂直于x轴于点C，记点P关于y轴的对称点为Q.
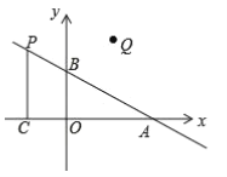
(1)当b=1时:①求直线AB相应的函数表达式:②若
，求点P的坐标:
(2)设点P的横坐标为a，是否同时存在a、b，使得
是等腰直角三角形?若存在，求出所有满足条件的a、b的值；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com