
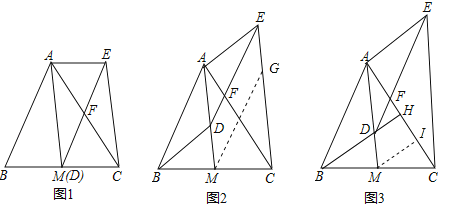
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合)DE∥AB交AC于点F,CE∥AM,连结AE.
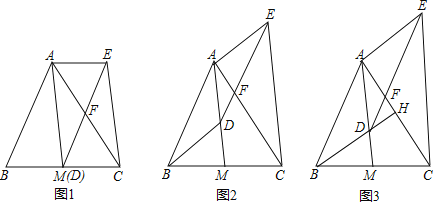
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM
①求∠CAM的度数;
②当FH=![]() , DM=4时,求DH的长.
, DM=4时,求DH的长.
【答案】(1)证明见解析;(2)证明见解析;(3)见解析.
【解析】试题分析:(1)只要证明AE=BM,AE∥BM即可解决问题;
(2)成立.如图2中,过点M作MG∥DE交CE于G.由四边形DMGE是平行四边形,推出ED=GM,且ED∥GM,由(1)可知AB=GM,AB∥GM,可知AB∥DE,AB=DE,即可推出四边形ABDE是平行四边形;
(3)①如图3中,取线段HC的中点I,连接MI,只要证明MI=![]() AM,MI⊥AC,即可解决问题;
AM,MI⊥AC,即可解决问题;
②设DH=x,则AH=![]() x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出
x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出![]() ,可得
,可得![]() ,解方程即可;
,解方程即可;
试题解析:(1)如图1中,∵DE∥AB,∴∠EDC=∠ABM,
∵CE∥AM,∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,∴BD=DC,∴△ABD≌△EDC,
∴AB=ED,∵AB∥ED,∴四边形ABDE是平行四边形.
(2)结论:成立.理由如下:
如图2中,过点M作MG∥DE交CE于G.
∵CE∥AM,∴四边形DMGE是平行四边形,∴ED=GM,且ED∥GM,
由(1)可知AB=GM,AB∥GM,∴AB∥DE,AB=DE,∴四边形ABDE是平行四边形;
(3)①如图3中,取线段HC的中点I,连接MI,
∵BM=MC,∴MI是△BHC的中位线,∴MI∥BH,MI=![]() BH,
BH,
∵BH⊥AC,且BH=AM,∴MI=![]() AM,MI⊥AC,∴∠CAM=30°.
AM,MI⊥AC,∴∠CAM=30°.
②设DH=x,则AH=![]() x,AD=2x,∴AM=4+2x,∴BH=4+2x,
x,AD=2x,∴AM=4+2x,∴BH=4+2x,
∵四边形ABDE是平行四边形,∴DF∥AB,∴![]() ,
,
∴![]() ,解得x=
,解得x=![]() 或
或![]() (舍弃),
(舍弃),
∴DH=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为19,点D,E在边BC上,∠ABC的平分线垂直于AE,垂足为N,∠ACB的平分线垂直于AD,垂足为M,若BC=7,则MN的长度为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC=![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;

(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.

(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△OC′D的周长;
(3)点M是第一象限内抛物线上的一动点,问:点M在何处时;△AMA′的面积最大?最大面积是多少?并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省嘉兴市,第20题,8分)如图,一次函数![]() (
(![]() )与反比例函数
)与反比例函数![]() (
(![]() )的图象交于点A(﹣1,2),B(m,﹣1).
)的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚同学动手剪了如图①所示![]() ,
,![]() 的正方形纸片与
的正方形纸片与![]() 的长方形纸片若干块.
的长方形纸片若干块.
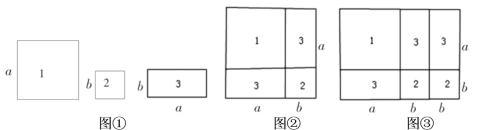
(1)小刚用1张1号、1张2号和2张3号纸片拼出一个新图形(如图②),根据这个图形的面积关系可以写出一个你所熟悉的乘法公式,这个乘法公式是 ;
(2)根据小刚用1张1号、2张2号和3张3号纸片拼成的长方形(如图③),6张纸片的面积等于所拼成大长方形的面积,将多项式![]() 因式分解,其结果是 ;
因式分解,其结果是 ;
(3)动手操作,请你依照小刚的方法,利用拼图分解因式:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
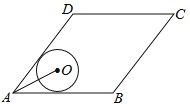
A.5 B.6 C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月20日是中国学生营养日,按时吃早餐是一种健康的饮食习惯.为了解本校七年级学生饮食习惯,李明和同学们在七年级随机调查了一部分学生每天吃早餐的情况,并将统计结果绘制成如下统计图(不完整).图中![]() 表示不吃早餐,
表示不吃早餐,![]() 表示偶尔吃早餐,
表示偶尔吃早餐,![]() 表示经常吃早餐,
表示经常吃早餐,![]() 表示每天吃早餐.请根据统计图解答以下问题:
表示每天吃早餐.请根据统计图解答以下问题:
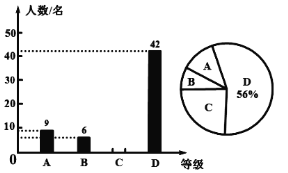
(1)这次共调查了多少名学生?
(2)请补全条形统计图;
(3)这个学校七年级共有学生1200名,请估计这个学校七年级每天约有多少名学生不吃早餐?
(4)请根据此次调查结果提一条合理的建议。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某铁路桥长1000米.现有一列火车从桥上匀速通过.测得火车从开始上桥到完全通过桥共用了1分钟(即从车头进入桥头到车尾离开桥尾),整个火车完全在桥上的时间为40秒.
(1)如果设这列火车的长度为x米,填写下表(不需要化简):
火车行驶过程 | 时间(秒) | 路程(米) | 速度(米/秒) |
完全通过桥 | 60 | ||
整列车在桥上 | 40 |
(2)求这列火车的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com