
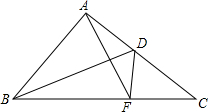
 已知:在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,F为BC上一点,且∠ADB=∠CDF,连接AF.求证:AF⊥BD.
已知:在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,F为BC上一点,且∠ADB=∠CDF,连接AF.求证:AF⊥BD. 分析 作AM⊥BC交BD于H,易证△AHD≌△CFD,得到AH=CF,可证明△ABH≌△CAF,得到∠1=∠2,由∠2+∠BAF=90°得到∠1+∠BAF=90°,所以AF⊥BD.
解答 证明:作AM⊥BC交BD于H,
∵D为AC的中点,
∴AD=DC,
∵AB=AC,∠BAC=90°,
∴∠HAD=∠C=∠BAH=45°,
在△AHD和△CFD中,
$\left\{\begin{array}{l}{∠HAD=∠C}\\{AD=DC}\\{∠ADB=∠CDF}\end{array}\right.$,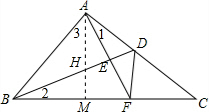
∴△AHD≌△CFD,
∴AH=CE,
在△ABH和△CAF中,
$\left\{\begin{array}{l}{AH=CE}\\{∠C=∠BAH}\\{AB=AC}\end{array}\right.$,
∴△ABH≌△CAF,
∴∠1=∠2,
∵∠2+∠BAF=90°,
∴∠1+∠BAF=90°,
∴∠AEB=90°,
∴AF⊥BD.
点评 本题考查了全等三角形的判定与性质,通过辅助线构造出两对全等三角形是解决问题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:填空题
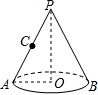 小明在圣诞节前做了一顶圆锥形纸帽PAB(如图),底面周长=14πcm,母线PA=28cm,一根彩带从母线PA的中点C开始绕圆锥形纸帽PAB的侧面到A点,则彩带长至少需14$\sqrt{5}$cm.
小明在圣诞节前做了一顶圆锥形纸帽PAB(如图),底面周长=14πcm,母线PA=28cm,一根彩带从母线PA的中点C开始绕圆锥形纸帽PAB的侧面到A点,则彩带长至少需14$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
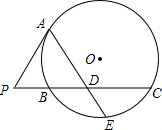 如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B、C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:
如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B、C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
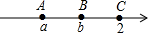 如图,A、B、C在数轴上对应的数分别为a、b和2,AB=BC,若|a|>2,|b|<2,那么原点的位置应该在( )
如图,A、B、C在数轴上对应的数分别为a、b和2,AB=BC,若|a|>2,|b|<2,那么原点的位置应该在( )| A. | 点A在左边 | B. | 点B和点C之间且靠近点C | ||
| C. | 点B和点C之间且靠近点B | D. | 点C的右边 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com