
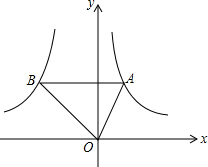
 ��ͼ����A�Ƿ���������y1=$\frac{2}{x}$��x��0��ͼ���ϵ�����һ�㣬����A�� AB��x�ᣬ����һ����������y2=$\frac{k}{x}$��k��0��x��0����ͼ���ڵ�B��
��ͼ����A�Ƿ���������y1=$\frac{2}{x}$��x��0��ͼ���ϵ�����һ�㣬����A�� AB��x�ᣬ����һ����������y2=$\frac{k}{x}$��k��0��x��0����ͼ���ڵ�B������ ��1��������AB��y���ڵ�C���ɵ�A�Ƿ���������y1=$\frac{2}{x}$��x��0��ͼ���ϵ�����һ�㣬AB��x�ᣬ����á�AOC����������ɡ�AOB���������3��������á�BOC��������̶����k��ֵ��
��2���ɵ�A�ĺ�������1������õ�A�����꣬�̶���õ�B�������꣬�����õ�B�����꣬������AB��OA��OB�ij���Ȼ���ɹ��ɶ������涨������á�AOB�Ķ�����
��3������y2=$\frac{k}{x}$����һ��D��ʹ�ı���AOBDΪƽ���ı��Σ���D��DE��AB����A��AC��x�ᣬ���ı���AOBDΪƽ���ı��Σ�����ƽ���ı��εĶԱ�ƽ������ȣ�����AAS�õ�������AOC��������DBEȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ�BE=OC��DE=AC����A��a��$\frac{2}{a}$����a��0������OC=a��AC=$\frac{2}{a}$���ó�D��B�����꣬������ʾ��D��B�����꣬��������֮��ľ���ֵ��ΪBE�ij������õ�ʽ���������k��ֵ��
��� 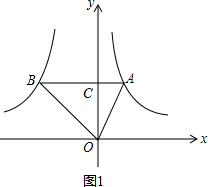 �⣺��1����ͼ1����AB��y���ڵ�C��
�⣺��1����ͼ1����AB��y���ڵ�C��
�ߵ�A�Ƿ���������y1=$\frac{2}{x}$��x��0��ͼ���ϵ�����һ�㣬��AB��x�ᣬ
��AB��y�ᣬ
��S��AOC=$\frac{1}{2}$��2=1��
��S��AOB=3��
��S��BOC=2��
��k=-4��
�ʴ�Ϊ��-4��
��2���ߵ�A�ĺ�������1��
��y=$\frac{2}{1}$=2��
���A��1��2����
��AB��x�ᣬ
���B��������Ϊ2��
��2=-$\frac{8}{x}$��
��ã�x=-4��
���B��-4��2����
��AB=AC+BC=1+4=5��OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$��OB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��
��OA2+OB2=AB2��
���AOB=90�㣻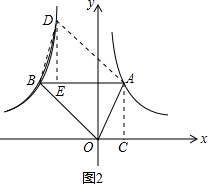 ��3���⣺����y2=$\frac{k}{x}$����һ��D��ʹ�ı���AOBDΪƽ���ı��Σ�
��3���⣺����y2=$\frac{k}{x}$����һ��D��ʹ�ı���AOBDΪƽ���ı��Σ�
��D��DE��AB����A��AC��x�ᣬ
���ı���AOBDΪƽ���ı��Σ�
��BD=OA��BD��OA��
���DBA=��OAB=��AOC��
�ڡ�AOC�͡�DBE�У�
$\left\{\begin{array}{l}{��DBE=��AOC}\\{��DEB=��ACO=90��}\\{DB=AO}\end{array}\right.$��
���AOC�ա�DBE��AAS����
��A��a��$\frac{2}{a}$����a��0������OC=a��AC=$\frac{2}{a}$��
��BE=OC=a��DE=AC=$\frac{2}{a}$��
��D������Ϊ$\frac{4}{a}$��B������Ϊ$\frac{2}{a}$��
��D������Ϊ$\frac{ak}{4}$��B������Ϊ$\frac{ak}{2}$��
��BE=|$\frac{ak}{4}$-$\frac{ak}{2}$|=a����-$\frac{ak}{4}$=a��
��k=-4��
���� �������ڷ����������ۺ��⣬�����˷�����������ϵ��k�ļ������塢���ɶ������涨����ȫ�������ε��ж��������Լ�ƽ���ı��ε����ʣ�ע��ڣ�3�����У���A��a��$\frac{2}{a}$����a��0�����ٷֱ��ʾ������������ǹؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
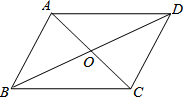 ��ͼ��?ABCD���ܳ���28cm����ABC���ܳ���22cm���Խ��߽��ڵ�O����OC�ij�Ϊ4cm��
��ͼ��?ABCD���ܳ���28cm����ABC���ܳ���22cm���Խ��߽��ڵ�O����OC�ij�Ϊ4cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}\sqrt{3}$ | B�� | 16$\sqrt{3}$ | C�� | 64$\sqrt{3}$ | D�� | 8$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com