
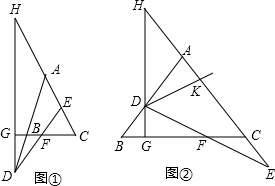
 已知:如图,在△ABC中,AB=AC,点D,E分别是射线AB,射线AC上一动点,连接DE交BC于点F,且DF=EF,过点DG⊥CB交射线CB于点G,交CA的延长线于点H.
已知:如图,在△ABC中,AB=AC,点D,E分别是射线AB,射线AC上一动点,连接DE交BC于点F,且DF=EF,过点DG⊥CB交射线CB于点G,交CA的延长线于点H.分析 (1)作EM∥AB,得到∠ABC=∠EMC,进而判断出△DBF≌△EMF,得到AD=AB+DB即可;
(2)作FP⊥AC于P,先判断△ABC为等边三角形得到∠B=∠ACB=60°,由DG⊥BC可得∠BDG=30°,∠H=30°,根据对顶角相等得到∠ADH=30°,再根据折叠的性质得∠DKH=90°,设CF=3x,则CK=5x,由于FD=FE,FP⊥EK,DK⊥AC,则PE=PK,PF为△EDK的中位线,即可,
解答 解:(1)如图①,
过点E作EM∥AB,
∴∠ABC=∠EMC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EMC=∠ACB
∴EM=EC,
∵∠DBF=180°-∠ABC,
∠EMF=180°-∠EMC,
∴∠DBF=∠EMF,
在△DBF和△EMF中,
$\left\{\begin{array}{l}{∠DBF=∠EMF}\\{∠BFD=∠EFM}\\{DF=EF}\end{array}\right.$,
∴△DBF≌△EMF,
∴BD=EM,
∵EM=EC,
∴BD=EC,
∵DG⊥BC,
∴∠HDA+∠DBG=90°,
∵∠DBG=∠ABC=∠ACB,
∴∠HDA+∠ACB=90°,
∵∠DHC+∠ACB=90°,
∴∠HDA=∠DHC,
∴AH=AD,
∵AD=AB+BD=AC+EC,
∴AH=AC+EC,
∴AH-EC=AC;
(2)解:作FP⊥AC于P,如图2,
∵∠BAC=60°,AB=AC,
∴△ABC为等边三角形,
∴∠B=∠ACB=60°,
∵DG⊥BC,
∴∠BDG=30°,∠H=30°,
∴∠ADH=30°,
∵将∠ADH沿直线AD翻折交AC于点K,
∴∠ADK=∠ADH=30°,
∴∠DKH=90°,
设CF=3x,则CK=5x,
∵FD=FE,FP⊥EK,
而DK⊥AC,
∴PE=PK,PF为△EDK的中位线,
∴PK=$\frac{1}{2}$KE=$\frac{1}{2}$×$\frac{14}{3}$=$\frac{7}{3}$,
∴PC=CK-PK=5x-$\frac{7}{3}$,
在Rt△PCF中,∠PCF=60°,∠PFC=30°,
∴FC=2PC,即3x=2(5x-$\frac{7}{3}$),
∴x=$\frac{2}{3}$,
∴PC=5×$\frac{2}{3}$-$\frac{7}{3}$=1,FC=2,
∴PF=$\sqrt{3}$PC=$\sqrt{3}$,
∴DK=2PF=2$\sqrt{3}$,
在Rt△ADK中,∠ADK=30°,
∴AK=$\frac{\sqrt{3}}{3}$DK=2,AD=2AK=4,
∴AC=AK+CK=2+5×$\frac{2}{3}$=$\frac{16}{3}$,
∴AB=$\frac{16}{3}$,
∴BD=AB-AD=$\frac{16}{3}$-4=$\frac{4}{3}$,
在Rt△BDG中,∠BDG=30°,
∴BG=$\frac{1}{2}$BD=$\frac{2}{3}$.
点评 此题是几何变换综合题,本题考查了折叠的性质,也考查了等腰三角形,等边三角形的性质和含30度的直角三角形三边的关系.作出辅助线是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:填空题
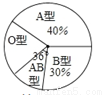
小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.
如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
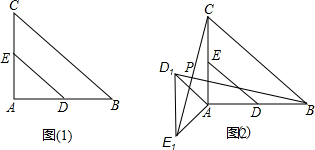 如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
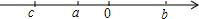 已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.
已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
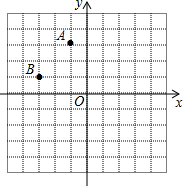 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com