
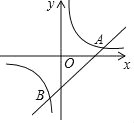
【题目】如图,一次函数y=kx+b(k≠0)和反比例函数y=![]() (m≠0)分别交于点A(4,1),B(﹣1,a)
(m≠0)分别交于点A(4,1),B(﹣1,a)
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出kx+b>![]() 的x的取值范围.
的x的取值范围.
【答案】(1)y=![]() ;y=x-3;(2)S△AOB=
;y=x-3;(2)S△AOB=![]() ;(3)x>4或-1<x<0.
;(3)x>4或-1<x<0.
【解析】
(1)把点A(4,1)与点B(-1,n)代入反比例函数y=![]() 得到m=4,即反比例函数的解析式为y=
得到m=4,即反比例函数的解析式为y=![]() ,把点A(4,1)与点B(-1,-4)代入一次函数y=kx+b,得到
,把点A(4,1)与点B(-1,-4)代入一次函数y=kx+b,得到![]() ,解得:
,解得:![]() 得到一次函数解析式为y=x-3;(2)根据三角形的面积公式即可得到结论;(3)由图象即可可得结论.
得到一次函数解析式为y=x-3;(2)根据三角形的面积公式即可得到结论;(3)由图象即可可得结论.
(1)解:∵点A(4,1)与点B(-1,n)在反比例函数y=![]() (m≠0)图象上,
(m≠0)图象上,
∴m=4,即反比例函数的解析式为y=![]() ,
,
当x=1时,n=-4,即B(-1,-4),
∵点A(4,1)与点B(-1,-4)在一次函数y=kx+b(k≠0)图象上,
∴![]() ,解得:
,解得:![]()
∴一次函数解析式为y=x-3;
(2)解:对于y=x-3,当y=0时,x=3,
∴C(3,0)
∴S△AOB=S△AOC+S△BOC=![]() ;
;
(3)解:由图象可得,当-1<x<0或x>4时,一次函数的值大于反例函数的值.


科目:初中数学 来源: 题型:
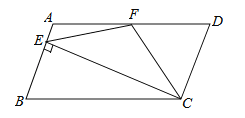
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E不与A、B重合),连接EF、CF,则下列结论中一定成立的是 ( )
①∠DCF=![]() ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③![]() ;④∠DFE=4∠AEF.
;④∠DFE=4∠AEF.
A. ①②③④ B. ①②③ C. ①② D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
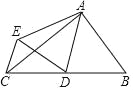
【题目】如图,△ABC 中,∠BAC=9 0°,AB=3,AC=4,点 D 是 BC 的中点,将△ABD 沿 AD 翻折得到△AED,连 CE,则线段 CE 的长等于( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=120°,AC平分∠MAN.
(1)在图1中,若∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
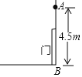
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
查看答案和解析>>
科目:初中数学 来源: 题型:
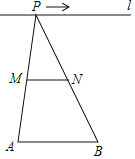
【题目】如图,已知线段![]() ,
,![]() 是直线
是直线![]() 上一动点,点
上一动点,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,对下列各值:①线段
的中点,对下列各值:①线段![]() 的长;②
的长;②![]() 的周长;③
的周长;③![]() 的面积;④直线
的面积;④直线![]() ,
,![]() 之间的距离;⑤
之间的距离;⑤![]() 的大小.其中不会随点
的大小.其中不会随点![]() 的移动而改变的是_____.(填序号)
的移动而改变的是_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
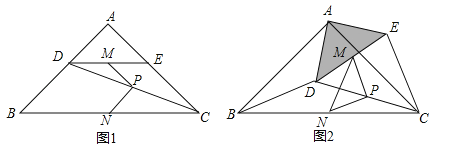
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
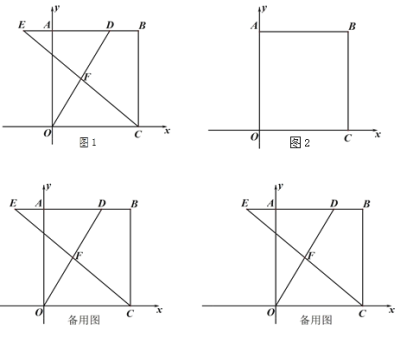
【题目】矩形OABC的顶点O与坐标原点重合,点B的坐标为(6,8),动点D、E分别从点B、A同时出发,沿射线BA运动,点D、E的运动速度均为每秒2个单位,设D、E的运动时间为t秒.连接OD、CE交于点F.
(1)如图1,求点F的纵坐标;
(2)若点G为OA的中点,在点D、E运动过程中,设△GEF的面积为y,求y与t的关系式;
(3)在(2)的条件下,连接BG,线段BG、OD交于点K,若![]() ,坐标平面内是否存在点M,使以D、E、K、M为顶点的四边形为平行四边形,如果存在,请求出点M的坐标;如果不存在,请说明理由.
,坐标平面内是否存在点M,使以D、E、K、M为顶点的四边形为平行四边形,如果存在,请求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com