
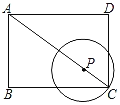
【题目】如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为__.
【答案】![]() 或
或![]()
【解析】
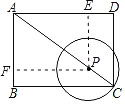
作PE⊥AD于E,PF⊥AB于F,根据勾股定理求出AC,分⊙P与AD相切、⊙P与AB相切相切两种情况,根据相似三角形的判定定理和性质定理计算.
解:作PE⊥AD于E,PF⊥AB于F,
在Rt△ABC中,AC=![]() =5,
=5,
由题意可知,⊙P只能与矩形ABCD的边AD、AB相切,
当⊙P与AD相切时,PE=PC,
∵PE⊥AD,CD⊥AD,
∴PE//CD,
∴△APE∽△ACD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,CP=![]() ,
,
当⊙P与AB相切时,PF=PC,
∵PF⊥AB,CB⊥AB,
∴PF//BC,
∴△APE∽△ACD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,CP=![]() ,
,
综上所述,当⊙P与矩形ABCD的边相切时,CP的长![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某班甲、乙、丙三名同学20天的体温数据记录如下表:
甲的体温 | 乙的体温 | 丙的体温 | ||||||||||||
温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 |
频数 | 5 | 5 | 5 | 5 | 频数 | 6 | 4 | 4 | 6 | 频数 | 4 | 6 | 6 | 4 |
则在这20天中,甲、乙、丙三名同学的体温情况最稳定的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
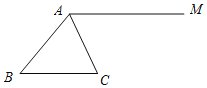
【题目】如图,AM∥BC,且AC平分∠BAM.
(1)用尺规作∠ABC的平分线BD交AM于点D,连接CD.(只保留作图痕迹,不写作法)
(2)求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=α,A为射线OM上一定点,OA=5,B为射线ON上一动点,连接AB,满足∠OAB,∠OBA均为锐角.点C在线段OB上(与点O,B不重合),满足AC=AB,点C关于直线OM的对称点为D,连接AD,OD.
(1)依题意补全图1;
(2)求∠BAD的度数(用含α的代数式表示);
(3)若tanα=![]() ,点P在OA的延长线上,满足AP=OC,连接BP,写出一个AB的值,使得BP∥OD,并证明.
,点P在OA的延长线上,满足AP=OC,连接BP,写出一个AB的值,使得BP∥OD,并证明.
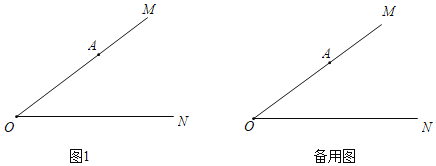
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y![]() x2bxc与直线y
x2bxc与直线y![]() x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
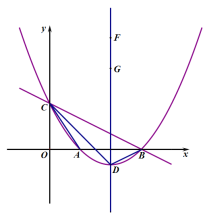
(1)求该抛物线的函数表达式;
(2)求该抛物线的对称轴和D点坐标;
(3)点F,G是对称轴上两个动点,且FG=2,点F在点G的上方,请直接写出四边形ACFG的周长的最小值;
(4)连接BD,若P在y轴上,且∠PBC=∠DBA+∠DCB,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明星期天上午8:00从家出发到离家36千米的书城买书,他先从家出发骑公共自行车到公交车站,等了12分钟的车,然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变,公交车匀速行驶,小明家、公交车站、书城依次在一条笔直的公路旁).如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象,其中线段AB对应的函教表达式为y=kx+6.
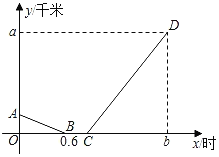
(1)求小明骑公共自行车的速度;
(2)求线段CD对应的函数表达式;
(3)求出发时间x在什么范围时,小明离公交车站的路程不超过3千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)当y2>y1时,求x的取值范围;
(3)求点B到直线OM的距离.
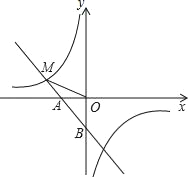
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在“爱护地球,绿化祖国”的活动中,组织同学开展植树造林活动,为了了解同学的植树情况,学校抽查了初一年级所有同学的植树情况(初一年级共有两个班),并将调查数据整理绘制成如下所示的部分数据尚不完整的统计图表.下面有四个推断:
初一年级植树情况统计表 | |||||
棵树/棵 | 1 | 2 | 3 | 4 | 5 |
人数 | 7 | 33 | a | 12 | 3 |
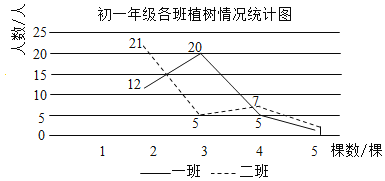
①a的值为20;
②初一年级共有80人;
③一班植树棵树的众数是3;
④二班植树棵树的是中位数2.
其中合理的是( )
A.①③B.②④C.②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线的对称轴;
(3)已知点![]() .若抛物线与线段
.若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com