
【题目】如图所示,抛物线y![]() x2bxc与直线y
x2bxc与直线y![]() x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
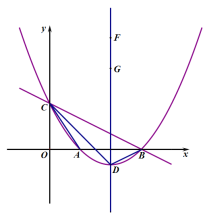
(1)求该抛物线的函数表达式;
(2)求该抛物线的对称轴和D点坐标;
(3)点F,G是对称轴上两个动点,且FG=2,点F在点G的上方,请直接写出四边形ACFG的周长的最小值;
(4)连接BD,若P在y轴上,且∠PBC=∠DBA+∠DCB,请直接写出点P的坐标.
【答案】(1)![]() ;(2)直线
;(2)直线![]() ;(3)
;(3)![]() ;(4)点P的坐标为
;(4)点P的坐标为![]() 或
或![]()
【解析】
(1)先根据直线![]() 求出B,C的坐标,然后利用待定系数法求抛物线的表达式即可;
求出B,C的坐标,然后利用待定系数法求抛物线的表达式即可;
(2)将抛物线的表达式变为顶点式,即可得到对称轴和D点坐标;
(3)因为AC,FG的值固定,所以只需找到![]() 的最小值即可,过点C作抛物线对称轴
的最小值即可,过点C作抛物线对称轴![]() 的对称点
的对称点![]() ,将
,将![]() 向下平移2个单位使F与点G重合,得到
向下平移2个单位使F与点G重合,得到![]() ,则
,则![]() ,当
,当![]() 三点共线时,
三点共线时,![]() 最小,最小值即为
最小,最小值即为![]() 的长度,通过勾股定理求出
的长度,通过勾股定理求出![]() 的值即可求解;
的值即可求解;
(4)分两种情况:当点P在y轴正半轴时和当点P在y轴负半轴时,首先通过锐角三角函数得出![]() ,从而得出
,从而得出![]() ,设
,设![]() ,则
,则![]() ,通过
,通过![]() 建立一个关于m的方程解方程即可求出PC的值,进而OP的长度即可,则P的坐标可求.
建立一个关于m的方程解方程即可求出PC的值,进而OP的长度即可,则P的坐标可求.
解:(1)令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
![]() ,
,
将点![]() 代入
代入![]() 中得,
中得,
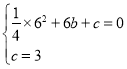 ,
,
解得![]()
∴抛物线的解析式为![]() ;
;
(2)∵![]() ,
,
∴抛物线的对称轴为![]() ,
,![]() ;
;
(3)∵抛物线的对称轴为![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,
,
![]()
∵四边形ACFG的周长为![]() ,而
,而![]() ,
,
∴只需找到![]() 的最小值即可,
的最小值即可,
过点C作抛物线对称轴![]() 的对称点
的对称点![]() ,将
,将![]() 向下平移2个单位使F与点G重合,得到
向下平移2个单位使F与点G重合,得到![]() ,则
,则![]() ,
,
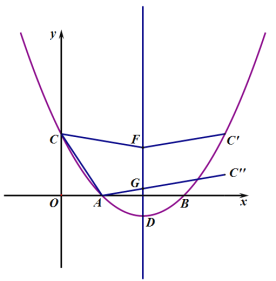
当![]() 三点共线时,
三点共线时,![]() 最小,最小值即为
最小,最小值即为![]() 的长度,
的长度,
![]() ,抛物线对称轴为
,抛物线对称轴为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴四边形ACFG的周长的最小值为![]() ;
;
(4)如图,当点P在y轴正半轴时,过点P作![]() 交BC的延长线于点Q,
交BC的延长线于点Q,
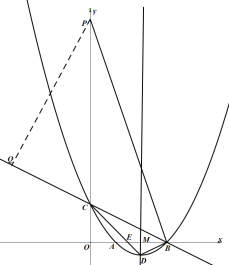
∵![]() ,
,
![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
![]() ,
,
解得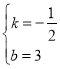 ,
,
∴直线CB解析式为![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
当点P在y轴负半轴时,如图,
同理可得![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上所述,点P的坐标为![]() 或
或![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
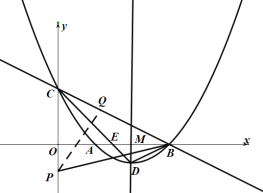
【题目】如图1,四边形ABCD为矩形,曲线L经过点D.点Q是四边形ABCD内一定点,点P是线段AB上一动点,作PM⊥AB交曲线L于点M,连接QM.
小东同学发现:在点P由A运动到B的过程中,对于x1=AP的每一个确定的值,θ=∠QMP都有唯一确定的值与其对应,x1与θ的对应关系如表所示:
x1=AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ=∠QMP | α | 85° | 130° | 180° | 145° | 130° |
小芸同学在读书时,发现了另外一个函数:对于自变量x2在﹣2≤x2≤2范围内的每一个值,都有唯一确定的角度θ与之对应,x2与θ的对应关系如图2所示:
根据以上材料,回答问题:
(1)表格中α的值为 .
(2)如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等,可以在两个变量x1与x2之间建立函数关系.
①在这个函数关系中,自变量是 ,因变量是 ;(分别填入x1和x2)
②请在网格中建立平面直角坐标系,并画出这个函数的图象;
③根据画出的函数图象,当AP=3.5时,x2的值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
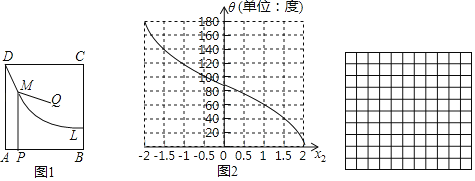
【题目】已知线段AB,如果将线段AB绕点A逆时针旋转90°得到线段AC,则称点C为线段AB关于点A的逆转点.点C为线段AB关于点A的逆转点的示意图如图1:
(1)如图2,在正方形ABCD中,点_____为线段BC关于点B的逆转点;
(2)如图3,在平面直角坐标系xOy中,点P的坐标为(x,0),且x>0,点E是y轴上一点,点F是线段EO关于点E的逆转点,点G是线段EP关于点E的逆转点,过逆转点G,F的直线与x轴交于点H.
①补全图;
②判断过逆转点G,F的直线与x轴的位置关系并证明;
③若点E的坐标为(0,5),连接PF、PG,设△PFG的面积为y,直接写出y与x之间的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=10,BC=15,tan∠A=![]() 点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
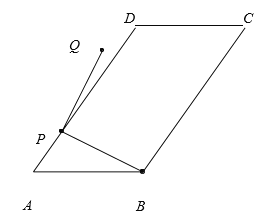
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为__.
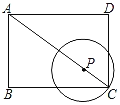
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为直径作
为直径作![]() ,点
,点![]() 为线段
为线段![]() 上一动点(与点O、A不重合),作
上一动点(与点O、A不重合),作![]() 于
于![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)求点![]() 的坐标和
的坐标和![]() 的值;
的值;
(2)设![]() .
.
①当![]() 时,求
时,求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
②求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(3)如图2,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,求
上运动时,求![]() 的最大值.
的最大值.
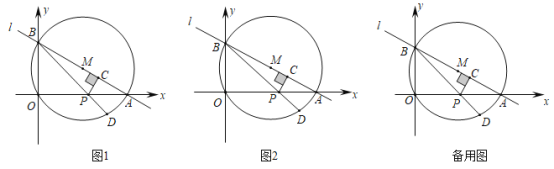
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆![]() 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.

小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地扶贫人员甲从办公室出发,骑车匀速前往所![]() 村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往
村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往![]() 村.甲、乙两人相距的路程
村.甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列三个说法:
(分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列三个说法:

①甲出发10分钟后与乙相遇;
②甲的速度是400米/分;
③乙返回办公室用时4分钟.
其中所有正确说法的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com