
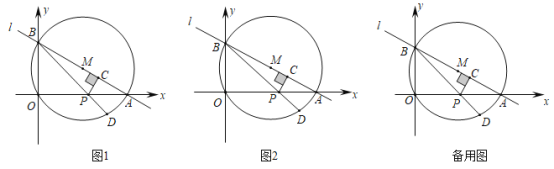
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为直径作
为直径作![]() ,点
,点![]() 为线段
为线段![]() 上一动点(与点O、A不重合),作
上一动点(与点O、A不重合),作![]() 于
于![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)求点![]() 的坐标和
的坐标和![]() 的值;
的值;
(2)设![]() .
.
①当![]() 时,求
时,求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
②求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(3)如图2,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,求
上运动时,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;
;![]() =
=![]() ;(2)①
;(2)①![]() ,点
,点![]() 的坐标为
的坐标为![]() ;②
;②![]() ;(3)
;(3)![]() .
.
【解析】
(1)令x=0求出y值可得B点坐标,令y=0求出x值可得A点坐标;根据A、B坐标可知OA、OB的长,根据正切的定义即可得![]() 的值;
的值;
(2)①由x=1可得点C与点M重合,如图1,连接![]() ,作
,作![]() 于
于![]() ,设
,设![]() ,则
,则![]() ,由垂径定理可得PA=PB,利用勾股定理可求出a值,根据正切的定义即可得出y值,可得PA的长,由AB是直径可知
,由垂径定理可得PA=PB,利用勾股定理可求出a值,根据正切的定义即可得出y值,可得PA的长,由AB是直径可知![]() ,可得
,可得![]() ,即可求出AD、PD的长,利用面积法及勾股定理即可求出DH、PH的长,进而可得点D坐标;
,即可求出AD、PD的长,利用面积法及勾股定理即可求出DH、PH的长,进而可得点D坐标;
②如图2,作![]() 交
交![]() 轴于点
轴于点![]() ,可得
,可得![]() ,可求出OE=2,根据平行线分线段成比例定理可得
,可求出OE=2,根据平行线分线段成比例定理可得![]() ,可用x表示出OP的长,根据正切的定义即可得出y与x的关系式;
,可用x表示出OP的长,根据正切的定义即可得出y与x的关系式;
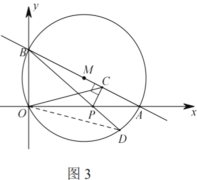
(3)如图3,连接![]() ,由
,由![]() 可证明
可证明![]() ,根据相似三角形的性质可得
,根据相似三角形的性质可得![]() ,即可证明
,即可证明![]() ,可得
,可得![]() ,进而可证明
,进而可证明![]() ,根据相似三角形的性质可得
,根据相似三角形的性质可得![]() ,设
,设![]() ,则
,则![]() ,即可用t表示出
,即可用t表示出![]() ,根据二次函数的性质即可求出
,根据二次函数的性质即可求出![]() 的最大值.
的最大值.
(1)∵![]() ,
,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴OA=8,OB=4,
∵![]() ,
,
∴![]() .
.
(2)①当![]() 时,
时,![]() ,
,
∴![]() ,即点
,即点![]() 与
与![]() 重合,
重合,
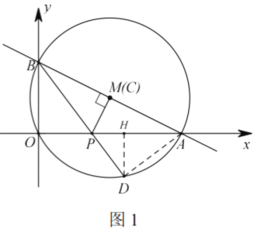
如图1,连接![]() ,作
,作![]() 于
于![]() ,设
,设![]() ,则
,则![]() ,
,
![]()
![]()
在![]() 中,
中,![]() ,
,
解得![]() ,
,
![]() ,
,
![]() 是
是![]() 的直径,
的直径,
∴![]()
∴![]() ,
,
设PD=x,则AD=![]() x,
x,
∴x2+(![]() x)2=52,
x)2=52,
解得:x=3,(负值舍去)即PD=3,
∴AD=![]() x=4,
x=4,
![]() ,
,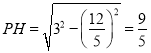 ,
,
![]() ,
,
∵点D在第四象限,
∴点![]() 的坐标为
的坐标为![]()
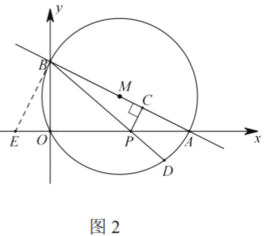
②如图2,作![]() 交
交![]() 轴于点
轴于点![]() ;
;
![]()
![]() ,
,
![]()
![]()
![]()
![]()
即![]()
![]()
![]()
![]() 关于
关于![]() 的函数表达式为
的函数表达式为![]()
(3)如图3,连接![]() ,
,
∵OA=8,OB=4,
∴AB=![]() ,
,
∵![]()
![]()
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知:△ABC为等边三角形.
(1)求作:△ABC的外接圆⊙O.(不写作法,保留作图痕迹)
(2)射线AO交BC于点D,交⊙O于点E,过E作⊙O的切线EF,与AB的延长线交于点F.
①根据题意,将(1)中图形补全;
②求证:EF∥BC;
③若DE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
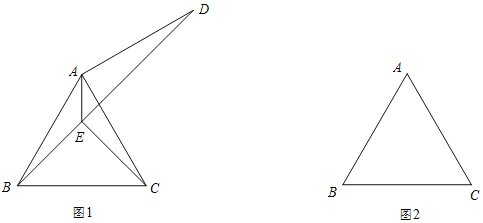
【题目】已知,如图,△ABC是等边三角形.
(1)如图1,将线段AC绕点A逆时针旋转90°,得到AD,连接BD,∠BAC的平分线交BD于点E,连接CE.
①求∠AED的度数;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果).
(2)如图2,将线段AC绕点A顺时针旋转90°,得到AD,连接BD,∠BAC的平分线交DB的延长线于点E,连接CE.
①依题意补全图2;
②用等式表示线段AE、CE、BD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y![]() x2bxc与直线y
x2bxc与直线y![]() x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
x3分别交于x轴,y轴上的B,C两点,设该抛物线与x轴的另一个交点为A,顶点为D,连接CD交x轴于点E.
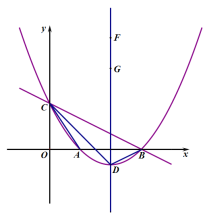
(1)求该抛物线的函数表达式;
(2)求该抛物线的对称轴和D点坐标;
(3)点F,G是对称轴上两个动点,且FG=2,点F在点G的上方,请直接写出四边形ACFG的周长的最小值;
(4)连接BD,若P在y轴上,且∠PBC=∠DBA+∠DCB,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校![]() 名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了如下不完整的频数表和频数直方图.
名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了如下不完整的频数表和频数直方图.
被抽取的部分学生安全知识测试成绩频数表
组别 | 成绩(分) | 频数(人) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
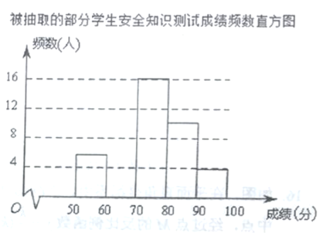
由图表中给出的信息回答下列问题:
![]() 表中的
表中的![]() ;抽取部分学生的成绩的中位数在 组;
;抽取部分学生的成绩的中位数在 组;
![]() 把上面的频数直方图补充完整;
把上面的频数直方图补充完整;
![]() 如果成绩达到
如果成绩达到![]() 分以上(包括
分以上(包括![]() 分)为优秀,请估计该校
分)为优秀,请估计该校![]() 名学生中成绩优秀的人数.
名学生中成绩优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
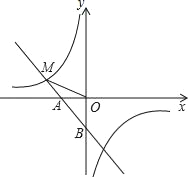
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)当y2>y1时,求x的取值范围;
(3)求点B到直线OM的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=x2﹣2mx+1图象与y轴的交点为A,将点A向右平移4个单位长度得到点B.
(1)直接写出点A与点B的坐标;
(2)求出抛物线的对称轴(用含m的式子表示);
(3)若函数y=x2﹣2mx+1的图象与线段AB恰有一个公共点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 |
|
|
|
|
|
|
|
人数 |
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 |
|
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 |
|
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com