
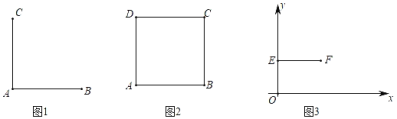
����Ŀ����֪�߶�AB��������߶�AB�Ƶ�A��ʱ����ת90���õ��߶�AC����Ƶ�CΪ�߶�AB���ڵ�A����ת�㣮��CΪ�߶�AB���ڵ�A����ת���ʾ��ͼ��ͼ1��
��1����ͼ2����������ABCD�У���_____Ϊ�߶�BC���ڵ�B����ת�㣻
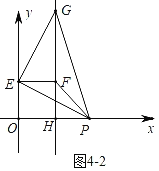
��2����ͼ3����ƽ��ֱ������ϵxOy�У���P������Ϊ��x��0������x��0����E��y����һ�㣬��F���߶�EO���ڵ�E����ת�㣬��G���߶�EP���ڵ�E����ת�㣬����ת��G��F��ֱ����x�ύ�ڵ�H��
�ٲ�ȫͼ��
���жϹ���ת��G��F��ֱ����x���λ�ù�ϵ��֤����
������E������Ϊ��0��5��������PF��PG�����PFG�����Ϊy��ֱ��д��y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
���𰸡���1��A����2���ٲ�ͼ����������GF��x�֤������������y=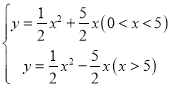 ��
��
��������
��1�����ݵ�CΪ�߶�AB���ڵ�A����ת��Ķ����жϼ��ɣ�
��2���ٰ���ɶ��岹ͼ���ɣ�
�ڽ��ۣ�GF��x�ᣮ֤����GEF�ա�PEO��SAS�����Ƴ���GFE����EOP��90���ɵý��ۣ�
�۷��������Σ���ͼ4��1�У���0��x��5ʱ����ͼ4��2�У���x��5ʱ���ֱ����������ε������ʽ��⼴�ɣ�
�⣺��1�������⣬��A���߶�AB���ڵ�B����ת�㣬
�ʴ�ΪA��
��2����ͼ����ͼ3��ʾ��
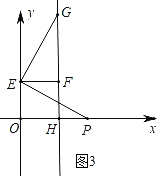
�ڽ��ۣ�GF��x�ᣮ
���ɣ��ߵ�F���߶�EF���ڵ�E����ת�㣬��G���߶�EP���ڵ�E����ת�㣬
���OEF����PEG��90����EG��EP��EF��EO��
���GEF����PEO��
���GEF�ա�PEO��SAS����
���GFE����EOP��
��OE��OP��
���POE��90����
���GFE��90����
�ߡ�OEF����EFH����EOH��90����
���ı���EFHO�Ǿ��Σ�
���FHO��90����
��FG��x�ᣮ
����ͼ4��1�У���0��x��5ʱ��
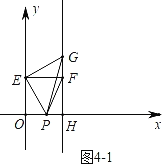
��E��0��5����
��OE��5��
���ı���EFHO�Ǿ��Σ�EF��EO��
���ı���EFHO�������Σ�
��OH��OE��5��
��y��![]() FGPH��
FGPH��![]() x��5��x������
x��5��x������![]() x2+
x2+![]() x��
x��
��ͼ4��2�У���x��5ʱ��
y��![]() FGPH��
FGPH��![]() x��x��5����
x��x��5����![]() x2��
x2��![]() x��
x��
����������y=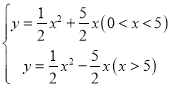 ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
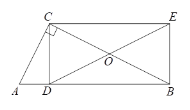
����Ŀ����ͼ����Rt��ABC�У���ACB=90����CD��AB��D��CE��AB��EB��CD������DE��BC�ڵ�O��
��1����֤��DE=BC��
��2�����AC=5��![]() ����DE�ij���
����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCΪ�ȱ������Σ�
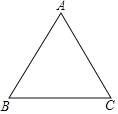
��1����������ABC�����Բ��O������д������������ͼ�ۼ���
��2������AO��BC�ڵ�D������O�ڵ�E����E����O������EF����AB���ӳ��߽��ڵ�F��
���������⣬����1����ͼ�β�ȫ��
����֤��EF��BC��
����DE��2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��ax2+4ax+b��a��0���Ķ���A��x���ϣ���y�ύ�ڵ�B��
��1���ú�a�Ĵ���ʽ��ʾb��
��2������BAO��45������a��ֵ��
��3���ᡢ�����궼�������ĵ�������㣮���������ڵ�A��B֮��IJ������߶�AB��Χ�ɵ��������߽磩��ǡ��û�����㣬��Ϻ�����ͼ��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
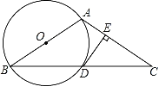
����Ŀ����֪����ͼ���ڡ�ABC�У���B����C����ABΪֱ���ġ�O��BC�ڵ�D������D��DE��AC�ڵ�E��
��1����֤��DE���O���У�
��2���ӳ�DE��BA���ӳ����ڵ�F����AB��8��sinB��![]() �����߶�FA�ij���
�����߶�FA�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
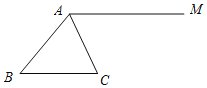
����Ŀ����ͼ��AM��BC����ACƽ�֡�BAM��
��1���ó߹�����ABC��ƽ����BD��AM�ڵ�D������CD����ֻ������ͼ�ۼ�����д������
��2����֤���ı���ABCD�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
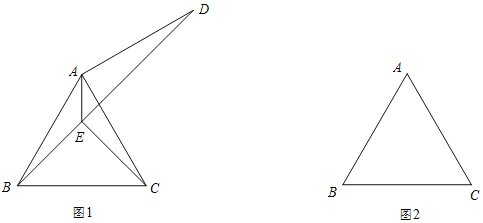
����Ŀ����֪����ͼ����ABC�ǵȱ������Σ�
��1����ͼ1�����߶�AC�Ƶ�A��ʱ����ת90�����õ�AD������BD����BAC��ƽ���߽�BD�ڵ�E������CE��
�����AED�Ķ�����
���õ�ʽ��ʾ�߶�AE��CE��BD֮���������ϵ��ֱ��д���������
��2����ͼ2�����߶�AC�Ƶ�A˳ʱ����ת90�����õ�AD������BD����BAC��ƽ���߽�DB���ӳ����ڵ�E������CE��
�������ⲹȫͼ2��
���õ�ʽ��ʾ�߶�AE��CE��BD֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������y![]() x2bxc��ֱ��y
x2bxc��ֱ��y![]() x3�ֱ���x�ᣬy���ϵ�B��C���㣬�����������x�����һ������ΪA������ΪD������CD��x���ڵ�E��
x3�ֱ���x�ᣬy���ϵ�B��C���㣬�����������x�����һ������ΪA������ΪD������CD��x���ڵ�E��
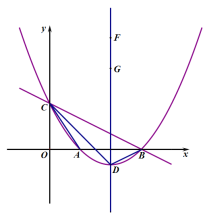
��1����������ߵĺ�������ʽ��
��2����������ߵĶԳ����D�����ꣻ
��3����F��G�ǶԳ������������㣬��FG=2����F�ڵ�G���Ϸ�����ֱ��д���ı���ACFG���ܳ�����Сֵ��
��4������BD����P��y���ϣ��ҡ�PBC=��DBA+��DCB����ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У����κ���y��x2��2mx+1ͼ����y��Ľ���ΪA������A����ƽ��4����λ���ȵõ���B��
��1��ֱ��д����A���B�����ꣻ
��2����������ߵĶԳ��ᣨ�ú�m��ʽ�ӱ�ʾ����
��3��������y��x2��2mx+1��ͼ�����߶�ABǡ��һ�������㣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com