
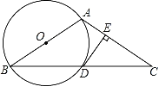
【题目】已知:如图,在△ABC中,∠B=∠C.以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE与⊙O相切;
(2)延长DE交BA的延长线于点F,若AB=8,sinB=![]() ,求线段FA的长.
,求线段FA的长.
【答案】(1)证明见解析;(2)FA=![]() .
.
【解析】
(1)要想证DE是⊙O的切线,只要连接OD,求证∠ODE=90°即可;
(2)连接AD,根据圆周角定理得到∠ADB=90°,根据三角函数的定义得到AD=ABsinB=![]() ,求得∠B=∠ADE,得到sinB=sin∠ADE=
,求得∠B=∠ADE,得到sinB=sin∠ADE=![]() =
=![]() ,求得AE=
,求得AE=![]() AD=
AD=![]() ×
×![]() =
=![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
(1)连接OD,则OD=OB,
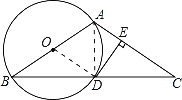
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C.
∴∠ODB=∠C,
∴OD∥AC.
∴∠ODE=∠DEC=90°,
∴DE是⊙O的切线;
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=8,sinB=![]() ,
,
∴AD=ABsinB=![]() ,
,
∵∠ODB+∠ADO=∠ADO+∠ADE=90°,
∴∠BDO=∠ADE,
∴∠B=∠ADE,
∴sinB=sin∠ADE=![]() =
=![]() ,
,
∴AE=![]() AD=
AD=![]() ×
×![]() =
=![]() ,
,
∵OD∥AE,
∴△FAE∽△FOD,
∴![]() ,
,

∵AB=8,
∴OD=AO=4,
∴![]() =
=![]()
∴FA=![]() .
.


科目:初中数学 来源: 题型:
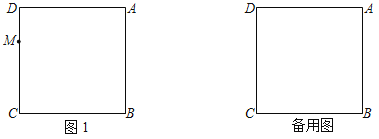
【题目】如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一笔总额为![]() 元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给
元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给![]() 个人,评一、二、三等奖的人数分别为
个人,评一、二、三等奖的人数分别为![]() ,且
,且![]() ,那么三等奖的奖金金额是_______元.
,那么三等奖的奖金金额是_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
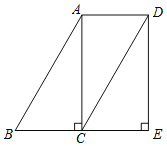
【题目】如图,在ABCD中,∠ACB=90°,过点D作DE⊥BC交BC的延长线于点E.
(1)求证:四边形ACED是矩形;
(2)连接AE交CD于点F,连接BF.若∠ABC=60°,CE=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,以AB边上的中线CD为直径作圆,如果与边AB有交点E(不与点D重合),那么称![]() 为△ABC的C﹣中线弧.例如,如图中
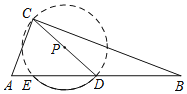
为△ABC的C﹣中线弧.例如,如图中![]() 是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
(1)当t=2时,
①在点C1(﹣3,2),C2(0,2![]() ),C3(2,4),C4(4,2)中,满足条件的点C是 ;
),C3(2,4),C4(4,2)中,满足条件的点C是 ;
②若在直线y=kx(k>0)上存在点P是△ABC的C﹣中线弧![]() 所在圆的圆心,其中CD=4,求k的取值范围;
所在圆的圆心,其中CD=4,求k的取值范围;
(2)若△ABC的C﹣中线弧![]() 所在圆的圆心为定点P(2,2),直接写出t的取值范围.
所在圆的圆心为定点P(2,2),直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
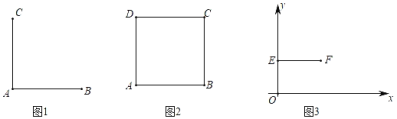
【题目】已知线段AB,如果将线段AB绕点A逆时针旋转90°得到线段AC,则称点C为线段AB关于点A的逆转点.点C为线段AB关于点A的逆转点的示意图如图1:
(1)如图2,在正方形ABCD中,点_____为线段BC关于点B的逆转点;
(2)如图3,在平面直角坐标系xOy中,点P的坐标为(x,0),且x>0,点E是y轴上一点,点F是线段EO关于点E的逆转点,点G是线段EP关于点E的逆转点,过逆转点G,F的直线与x轴交于点H.
①补全图;
②判断过逆转点G,F的直线与x轴的位置关系并证明;
③若点E的坐标为(0,5),连接PF、PG,设△PFG的面积为y,直接写出y与x之间的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
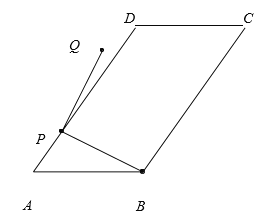
【题目】如图,在平行四边形ABCD中,AB=10,BC=15,tan∠A=![]() 点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
点P为AD边上任意一点,连结PB,将PB绕点P逆时针旋转90°得到线段PQ.若点Q恰好落在平行四边形ABCD的边所在的直线上,则PB旋转到PQ所扫过的面积____(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
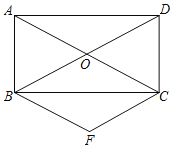
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,过B点作BF∥AC,过C点作CF∥BD,BF与CF相交于点F.
(1)求证:四边形BFCO是菱形;
(2)连接OF、DF,若AB=2,tan∠OFD=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com