
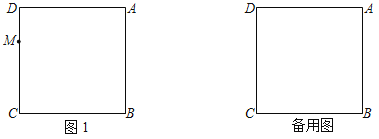
【题目】如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.
【答案】(1)详见解析;(2)![]() ;(3)1或
;(3)1或![]() .
.
【解析】
(1)根据题意作出图形便可,
(2)连接BM,先证明△ADM≌△ABF,再证明△FAE≌△MAB,求得BM,便可得EF;
(3)设DM=x(x>0),求出AE、AF、EF,当△AEF为等腰三角形,分两种情况:AE=EF或AF=EF,列出方程求出x的值,进而求得最后结果.
解:(1)根据题意作图如下:
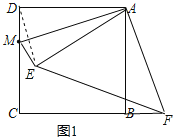
(2)连接BM,如图2,
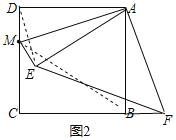
∵点D与点E关于AM所在直线对称,
∴AE=AD,∠MAD=∠MAE,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABF=90°,
∵BM=BF,
∴△ADM≌△ABF(SAS),
∴AF=AM,∠FAB=∠MAD,
∴∠FAB=∠NAE,
∴∠FAE=∠MAB,
∴△FAE≌△MAB(SAS),
∴EF=BM,
∵四边形ABCD是正方形,
∴BC=CD=AB=3,
∵DM=1,
∴CM=2,
∴BM=![]() ,
,
∴EF=![]() ;
;
(3)设DM=x(x>0),则CM=3﹣x,
∴EF=BM=![]() ,
,
∵AE=AD=3,AF=AM=![]() ,
,
∴AF>AE,
∴当△AEF为等腰三角形时,只能有两种情况:AE=EF,或AF=EF,
①当AE=EF时,有![]() =3,解得x=3
=3,解得x=3
∴tan∠DAM=![]() ;
;
②当AF=EF时,![]() =
=![]() ,解得,x=
,解得,x=![]() ,
,
∴tan∠DAM=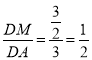 ,
,
综上,tan∠DAM的值为1或![]() .
.
故答案为:tan∠DAM的值为1或![]() .
.


科目:初中数学 来源: 题型:
【题目】某校为了解八年级学生参加社会实践活动情况,随机调查了本校部分八年级学生在第一学期参加社会实践活动的天数,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
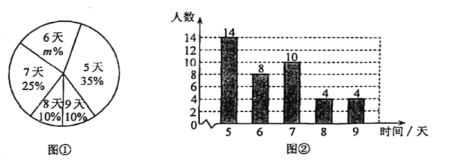
(1)本次接受随机抽样调查的学生人数为 ,图①中的![]() 的值为 ;
的值为 ;
(2)求本次抽样调查获取的样本数据的众数、中位数和平均数;
(3)若该校八年级学生有![]() 人,估计参加社会实践活动时间大于
人,估计参加社会实践活动时间大于![]() 天的学生人数.
天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种指甲剪.该指甲剪利用杠杆原理操作,使用者只需施力按压柄的末端,便可轻易透过锋利的前端刀片剪断指甲,它被按压后示意图如图2所示,上下臂![]()
![]() 杠杆
杠杆![]() 轴承
轴承![]() ,未使用指甲剪时,点
,未使用指甲剪时,点![]() 在
在![]() 上,且
上,且![]() 比
比![]() 长
长![]() ,则
,则![]() 的长为________
的长为________![]() ;使用指甲剪时,下压点
;使用指甲剪时,下压点![]() ,当
,当![]() 时,两刀片咬合,
时,两刀片咬合,![]() 绕点
绕点![]() 按逆时针方向旋转到
按逆时针方向旋转到![]() 的位置,则
的位置,则![]() 与
与![]() 的交点从开始到结束时移动的距离
的交点从开始到结束时移动的距离![]() 为_______
为_______![]()
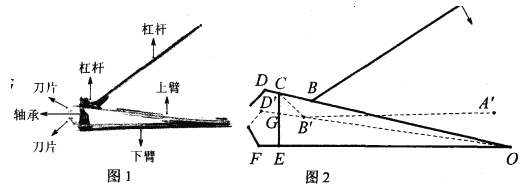
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)请在图①的![]() 的边
的边![]() 上求作一点
上求作一点![]() ,使
,使![]() 最短;
最短;
(2)如图②,点![]() 为
为![]() 内部一点,且满足
内部一点,且满足![]() .求证:点
.求证:点![]() 到点
到点![]() 、
、![]() 、
、![]() 的距离之和最短,即
的距离之和最短,即![]() 最短;
最短;
问题解决
(3)如图③,某高校有一块边长为400米的正方形草坪![]() ,现准备在草坪内放置一对石凳及垃圾箱在
,现准备在草坪内放置一对石凳及垃圾箱在![]() 点处,使点
点处,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和最小,那么是否存在符合条件的点
三点的距离之和最小,那么是否存在符合条件的点![]() ?若存在,请作出点
?若存在,请作出点![]() 的位置,并求出这个最短距离;若不存在,请说明理由.
的位置,并求出这个最短距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),
(m≠0,x>0)的图象在第一象限内交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为D,E.已知A(1,4),![]() =
=![]() .
.
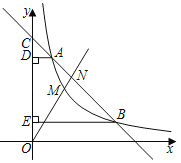
(1)求m的值和一次函数的解析式;
(2)若点M为反比例函数图象在A,B之间的动点,作射线OM交直线AB于点N,当MN长度最大时,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
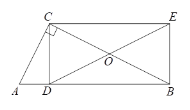
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE∥AB,EB∥CD,连接DE交BC于点O.
(1)求证:DE=BC;
(2)如果AC=5,![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
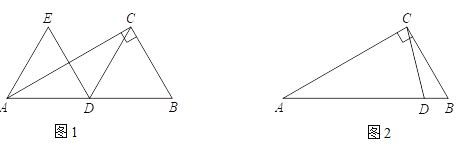
【题目】在△ABC中,∠ACB=90°,∠CAB=30°,点D在AB上,连接CD,并将CD绕点D逆时针旋转60°得到DE,连接AE.
(1)如图1,当点D为AB中点时,直接写出DE与AE长度之间的数量关系;
(2)如图2,当点D在线段AB上时,
① 根据题意补全图2;
② 猜想DE与AE长度之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
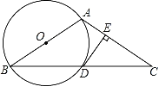
【题目】已知:如图,在△ABC中,∠B=∠C.以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE与⊙O相切;
(2)延长DE交BA的延长线于点F,若AB=8,sinB=![]() ,求线段FA的长.
,求线段FA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com