
【题目】在△ABC中,∠ACB=90°,∠CAB=30°,点D在AB上,连接CD,并将CD绕点D逆时针旋转60°得到DE,连接AE.
(1)如图1,当点D为AB中点时,直接写出DE与AE长度之间的数量关系;
(2)如图2,当点D在线段AB上时,
① 根据题意补全图2;
② 猜想DE与AE长度之间的数量关系,并证明.
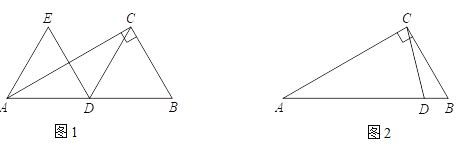
【答案】(1)DE=AE;(2)①补全图形见解析;②DE=AE,证明见解析.
【解析】
(1)想办法证明△ADE是等边三角形即可解决问题.
(2)①根据要求画出图形即可.
②首先证明△的长,△FBC都是等边三角形,再证明△ECF≌△DCB,推出∠4=∠5=60°,证明△EFA≌△EFC(SAS)可得结论.
解:(1)结论:DE=AE.
理由:如图1中,
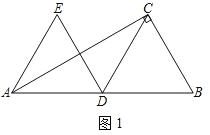
∵∠ACB=90°,∠BAC=30°,
∴AB=2BC,∠B=60°,
∵AD=DB,
∴CD=AD=DB,
∴△CDB是等边三角形,
∴∠CDB=60°,
∵DC=DE,∠CDE=60°,
∴∠ADE=180°﹣∠ED﹣∠CDB=60°,
∵DA=DC,DC=DE,
∴AD=DE,
∴△ADE是等边三角形,
∴DE=AE.
(2)①图形如图2所示:
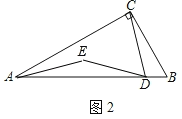
②如图2﹣1中,结论:DE=AE.
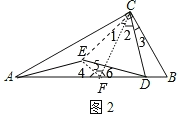
理由:取AB的中点F,连接CE,CF,EF.
∵∠ACB=90°,AF=BF,
∴CF=AF=BF,
∵∠B=60°,
∴△BCF是等边三角形,
∵DC=DE,∠CDE=60°,
∴△ECD是等边三角形,
∴∠1+∠2=∠2+∠3=60°,CE=CD,CF=CB,
∴∠1=∠3,
∴△ECF≌△DCB(SAS),
∴∠5=∠B=60°,
∵∠6=60°,
∴∠4=∠5=60°,
∵EF=EF,FA=FC,
∴△EFA≌△EFC(SAS),
∴AE=EC,
∵EC=ED,
∴AE=ED.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC,BD相交于点O,过点O作BD的垂线与边AD,BC分别交于点E,F,连接BE交AC于点K,连接DF.
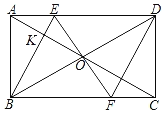
(1)求证:四边形EBFD是菱形;
(2)若BK=3EK,AE=4,求四边形EBFD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球已经进入大数据时代,大数据(bigdata)是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值.为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是根据调查结果绘制出不完整的两个统计图表:
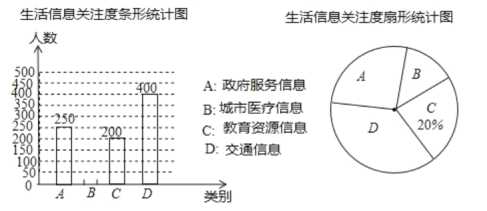
请根据图中提供的信息,解答下列问题:
(1)本次参与调查的人数是________,扇形统计图中![]() 部分的圆心角的度数是________,并补全条形统计图;
部分的圆心角的度数是________,并补全条形统计图;
(2)这次调查的市民最关心的四类生活信息的众数是________类;
(3)若我市现有常住人口约600万,请你估计最关心“城市医疗信息”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
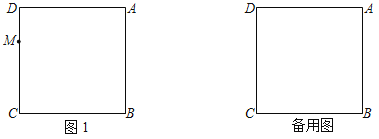
【题目】如图,在正方形ABCD中,AB=3,M是CD边上一动点(不与D点重合),点D与点E关于AM所在的直线对称,连接AE,ME,延长CB到点F,使得BF=DM,连接EF,AF.
(1)依题意补全图1;
(2)若DM=1,求线段EF的长;
(3)当点M在CD边上运动时,能使△AEF为等腰三角形,直接写出此时tan∠DAM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
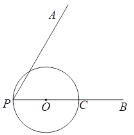
【题目】如图,∠APB,点C在射线PB上,PC为⊙O的直径,在∠APB内部且到∠APB两边距离都相等的所有的点组成图形M,图形M交⊙O于D,过点D作直线DE⊥PA,分别交射线PA,PB于E,F.
(1)根据题意补全图形;
(2)求证:DE是⊙O的切线;
(3)如果PC=2CF,且![]() ,求PE的长.
,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1) ,将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和1D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E 2F 2,如图(3) 中阴影部分;如此下去…,则正六角星形AnFnBnDnCnE nF n的面积为_______.
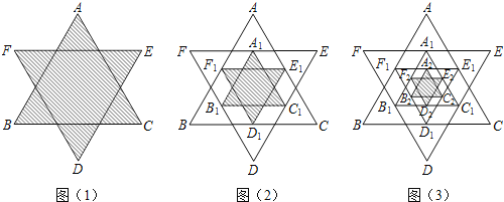
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的任意一点
中的任意一点![]() ,给出如下定义:经过点
,给出如下定义:经过点![]() 且平行于两坐标轴夹角平分线的直线,叫做点
且平行于两坐标轴夹角平分线的直线,叫做点![]() 的“特征线”.例如:点
的“特征线”.例如:点![]() 的特征线是
的特征线是![]() 和
和![]() .
.
(1)若点![]() 的其中一条特征线是
的其中一条特征线是![]() ,则在
,则在![]() 、
、![]() 、
、![]() 三个点中,可能是点
三个点中,可能是点![]() 的点有_______;
的点有_______;
(2)已知点![]() 的平行于第二、四象限夹角平分线的特征线与
的平行于第二、四象限夹角平分线的特征线与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() .使
.使![]() 的面积不小于6,求
的面积不小于6,求![]() 的取值范围;
的取值范围;
(3)已知点![]() ,
,![]() ,且
,且![]() 的半径为1.当
的半径为1.当![]() 与点
与点![]() 的特征线存在交点时,直接写出
的特征线存在交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一笔总额为![]() 元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给
元的奖金,分为一等奖、二等奖和三等奖,奖金金额均为整数,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍,若把这笔奖金发给![]() 个人,评一、二、三等奖的人数分别为
个人,评一、二、三等奖的人数分别为![]() ,且
,且![]() ,那么三等奖的奖金金额是_______元.
,那么三等奖的奖金金额是_______元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com