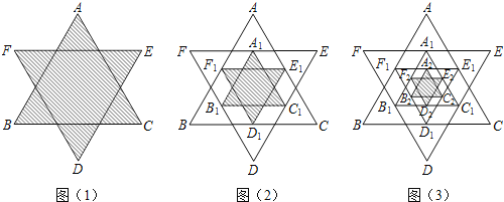
【题目】如图(1) ，将一个正六边形各边延长，构成一个正六角星形AFBDCE，它的面积为1，取△ABC和△DEF各边中点，连接成正六角星形A1F1B1D1C1E1，如图(2)中阴影部分；取△A1B1C1和1D1E1F1各边中点，连接成正六角星形A2F2B2D2C2E 2F 2，如图(3) 中阴影部分；如此下去…，则正六角星形AnFnBnDnCnE nF n的面积为_______.
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，点A，B，C的坐标分别是（0，4），（4，0），（8，0），⊙M是△ABC的外接圆，则点M的坐标为___________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题探究
（1）请在图①的
的边
上求作一点
，使
最短；
（2）如图②，点为内部一点，且满足
．求证：点到点
、
、
的距离之和最短，即
最短；
问题解决
（3）如图③，某高校有一块边长为400米的正方形草坪
，现准备在草坪内放置一对石凳及垃圾箱在点处，使点到、、
三点的距离之和最小，那么是否存在符合条件的点？若存在，请作出点的位置，并求出这个最短距离；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
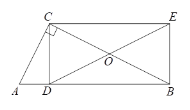
【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，CE∥AB，EB∥CD，连接DE交BC于点O．
（1）求证：DE=BC；
（2）如果AC=5，
，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
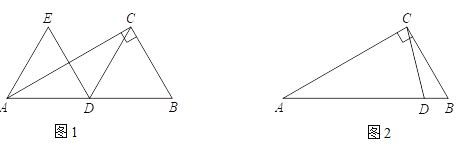
【题目】在△ABC中，∠ACB=90°，∠CAB=30°，点D在AB上，连接CD，并将CD绕点D逆时针旋转60°得到DE，连接AE．
（1）如图1，当点D为AB中点时，直接写出DE与AE长度之间的数量关系；
（2）如图2，当点D在线段AB上时，
① 根据题意补全图2；
② 猜想DE与AE长度之间的数量关系，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知抛物线
．
（1）抛物线的对称轴为_______；
（2）若当
时，
的最小值是
，求当时，的最大值；
（3）已知直线
与抛物线存在两个交点，设左侧的交点为点
，当
时，求
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：△ABC为等边三角形．
（1）求作：△ABC的外接圆⊙O．（不写作法，保留作图痕迹）
（2）射线AO交BC于点D，交⊙O于点E，过E作⊙O的切线EF，与AB的延长线交于点F．
①根据题意，将（1）中图形补全；
②求证：EF∥BC；
③若DE＝2，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
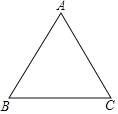
【题目】已知，如图，△ABC是等边三角形．
（1）如图1，将线段AC绕点A逆时针旋转90°，得到AD，连接BD，∠BAC的平分线交BD于点E，连接CE．
①求∠AED的度数；
②用等式表示线段AE、CE、BD之间的数量关系（直接写出结果）．
（2）如图2，将线段AC绕点A顺时针旋转90°，得到AD，连接BD，∠BAC的平分线交DB的延长线于点E，连接CE．
①依题意补全图2；
②用等式表示线段AE、CE、BD之间的数量关系，并证明．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
