
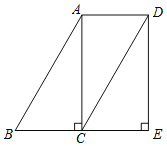
【题目】如图,在ABCD中,∠ACB=90°,过点D作DE⊥BC交BC的延长线于点E.
(1)求证:四边形ACED是矩形;
(2)连接AE交CD于点F,连接BF.若∠ABC=60°,CE=2,求BF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据四边形ABCD是平行四边形,可得AD∥BC.所以∠CAD=∠ACB=90°.又∠ACE=90°,即可证明四边形ACED是矩形;
(2)根据四边形ACED是矩形,和四边形ABCD是平行四边形,可以证明△ABE是等边三角形.再根据特殊角三角函数即可求出BF的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠CAD=∠ACB=90°.
又∵∠ACE=90°,DE⊥BC,
∴四边形ACED是矩形.
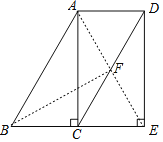
(2)解:∵四边形ACED是矩形,
∴AD=CE=2,AF=EF,AE=CD.
∵四边形ABCD是平行四边形,
∴BC=AD=2,AB=CD.
∴AB=AE.
又∵∠ABC=60°,
∴△ABE是等边三角形.
∴∠BFE=90°,![]() ,
,
在Rt△BFE中,![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】问题探究
(1)请在图①的![]() 的边
的边![]() 上求作一点
上求作一点![]() ,使
,使![]() 最短;
最短;
(2)如图②,点![]() 为
为![]() 内部一点,且满足
内部一点,且满足![]() .求证:点
.求证:点![]() 到点
到点![]() 、
、![]() 、
、![]() 的距离之和最短,即
的距离之和最短,即![]() 最短;
最短;
问题解决
(3)如图③,某高校有一块边长为400米的正方形草坪![]() ,现准备在草坪内放置一对石凳及垃圾箱在
,现准备在草坪内放置一对石凳及垃圾箱在![]() 点处,使点
点处,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和最小,那么是否存在符合条件的点
三点的距离之和最小,那么是否存在符合条件的点![]() ?若存在,请作出点
?若存在,请作出点![]() 的位置,并求出这个最短距离;若不存在,请说明理由.
的位置,并求出这个最短距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC为等边三角形.
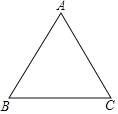
(1)求作:△ABC的外接圆⊙O.(不写作法,保留作图痕迹)
(2)射线AO交BC于点D,交⊙O于点E,过E作⊙O的切线EF,与AB的延长线交于点F.
①根据题意,将(1)中图形补全;
②求证:EF∥BC;
③若DE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区经过三年的新农村建设,年经济收入实现了翻两番(即是原来的22倍).为了更好地了解该地区的经济收入变化情况,统计了该地区新农村建设前后的年经济收入构成结构如图,则下列结论中不正确的是( )

A.新农村建设后,种植收入减少了
B.新农村建设后,养殖收入实现了翻两番
C.新农村建设后,第三产业收入比新农村建设前的年经济收入还多
D.新农村建设后,第三产业收入与养殖收入之和超过了年经济收入的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+4ax+b(a>0)的顶点A在x轴上,与y轴交于点B.
(1)用含a的代数式表示b;
(2)若∠BAO=45°,求a的值;
(3)横、纵坐标都是整数的点叫做整点.若抛物线在点A,B之间的部分与线段AB所围成的区域(不含边界)内恰好没有整点,结合函数的图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠B=∠C.以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE与⊙O相切;
(2)延长DE交BA的延长线于点F,若AB=8,sinB=![]() ,求线段FA的长.
,求线段FA的长.
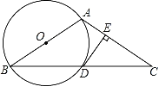
查看答案和解析>>
科目:初中数学 来源: 题型:
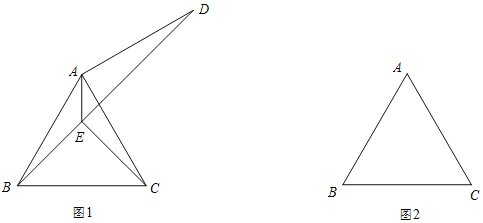
【题目】已知,如图,△ABC是等边三角形.
(1)如图1,将线段AC绕点A逆时针旋转90°,得到AD,连接BD,∠BAC的平分线交BD于点E,连接CE.
①求∠AED的度数;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果).
(2)如图2,将线段AC绕点A顺时针旋转90°,得到AD,连接BD,∠BAC的平分线交DB的延长线于点E,连接CE.
①依题意补全图2;
②用等式表示线段AE、CE、BD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,对角线AC,BD交于点O,E是边AD上的一个动点(与点A,D不重合),连接EO并延长,交BC于点F,连接BE,DF.下列说法:
① 对于任意的点E,四边形BEDF都是平行四边形;
② 当∠ABC>90°时,至少存在一个点E,使得四边形BEDF是矩形;
③ 当AB<AD时,至少存在一个点E,使得是四边形BEDF是菱形;
④ 当∠ADB=45°时,至少存在一个点E,使得是四边形BEDF是正方形.
所有正确说法的序号是:_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com