
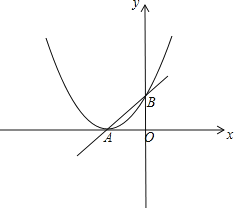
【题目】在平面直角坐标系xOy中,抛物线y=ax2+4ax+b(a>0)的顶点A在x轴上,与y轴交于点B.
(1)用含a的代数式表示b;
(2)若∠BAO=45°,求a的值;
(3)横、纵坐标都是整数的点叫做整点.若抛物线在点A,B之间的部分与线段AB所围成的区域(不含边界)内恰好没有整点,结合函数的图象,直接写出a的取值范围.
【答案】(1)b=4a;(2)![]() ;(3)
;(3)![]() 或a=1.
或a=1.
【解析】
(1)先将抛物线解析式化为顶点式,然后根据抛物线y=ax2+4ax+b(a>0)的顶点A在x轴上,可以得到该抛物线的顶点纵坐标为0,从而可以得到a和b的关系;
(2)根据抛物线解析式,可以得到点B的坐标为(0,4a),然后∠BAO=45°,可知4a=2,从而可以求得a的值;
(3)根据函数图象,可以写出a的取值范围.
解:(1)∵y=ax2+4ax+b=a(x+2)2+(b﹣4a),
∴该抛物线顶点A的坐标为(﹣2,b﹣4a),
∵顶点A在x轴上,
∴b﹣4a=0,
即b=4a;
(2)∵b=4a,
∴抛物线为y=ax2+4ax+4a(a>0),
∵抛物线顶点为A(﹣2,0),与y轴的交点B(0,4a)在y轴的正半轴,∠BAO=45°,
∴OB=OA=2,
∴4a=2,
∴![]() ;
;
(3)![]() 或a=1.
或a=1.
理由:∵点A(﹣2,0),点B(0,4a),
设直线AB的函数解析式为y=mx+n,
![]() ,得
,得![]() ,
,
即直线AB的解析式为y=2ax+4a,
∵抛物线解析式为y=ax2+4ax+4a(a>0),抛物线在点A,B之间的部分与线段AB所围成的区域(不含边界)内恰好没有整点,
∴![]() 或
或![]() ,
,
解得,a=1或0<a≤![]() ,
,
即a的取值范围是0<a≤![]() 或a=1.
或a=1.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程ax2+2x﹣3=0有两个不相等的实数根.
(1)求a的取值范围;
(2)若此方程的一个实数根为1,求a的值及方程的另一个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD为矩形,曲线L经过点D.点Q是四边形ABCD内一定点,点P是线段AB上一动点,作PM⊥AB交曲线L于点M,连接QM.
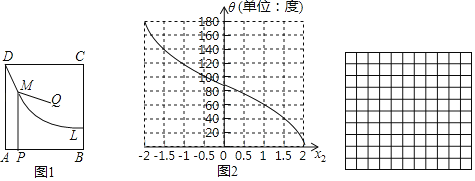
小东同学发现:在点P由A运动到B的过程中,对于x1=AP的每一个确定的值,θ=∠QMP都有唯一确定的值与其对应,x1与θ的对应关系如表所示:
x1=AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ=∠QMP | α | 85° | 130° | 180° | 145° | 130° |
小芸同学在读书时,发现了另外一个函数:对于自变量x2在﹣2≤x2≤2范围内的每一个值,都有唯一确定的角度θ与之对应,x2与θ的对应关系如图2所示:
根据以上材料,回答问题:
(1)表格中α的值为 .
(2)如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等,可以在两个变量x1与x2之间建立函数关系.
①在这个函数关系中,自变量是 ,因变量是 ;(分别填入x1和x2)
②请在网格中建立平面直角坐标系,并画出这个函数的图象;
③根据画出的函数图象,当AP=3.5时,x2的值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果![]() 的两个端点
的两个端点![]() 分别在
分别在![]() 的两边上(不与点
的两边上(不与点![]() 重合),并且
重合),并且![]() 除端点外的所有点都在
除端点外的所有点都在![]() 的内部,则称
的内部,则称![]() 是
是![]() 的“连角弧”.
的“连角弧”.
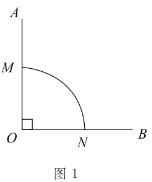
(1)图1中,![]() 是直角,
是直角,![]() 是以
是以![]() 为圆心,半径为1的“连角弧”.
为圆心,半径为1的“连角弧”.
①图中![]() 的长是______,并在图中再作一条以
的长是______,并在图中再作一条以![]() 为端点、长度相同的“连角弧”;
为端点、长度相同的“连角弧”;
②以![]() 为端点,弧长最长的“连角弧”的长度是_______.
为端点,弧长最长的“连角弧”的长度是_______.
(2)如图2,在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() 在
在![]() 轴正半轴上,若
轴正半轴上,若![]() 是半圆,也是
是半圆,也是![]() 的“连角弧”,求
的“连角弧”,求![]() 的取值范围.
的取值范围.

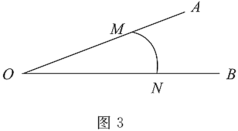
(3)如图3,已知点![]() 分别在射线
分别在射线![]() 上,
上,![]() 是
是![]() 的“连角弧”,且
的“连角弧”,且![]() 所在圆的半径为
所在圆的半径为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
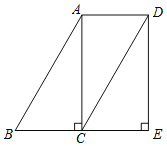
【题目】如图,在ABCD中,∠ACB=90°,过点D作DE⊥BC交BC的延长线于点E.
(1)求证:四边形ACED是矩形;
(2)连接AE交CD于点F,连接BF.若∠ABC=60°,CE=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
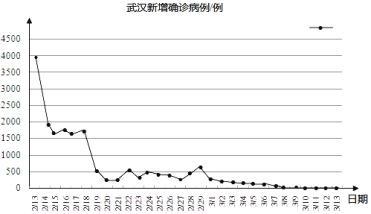
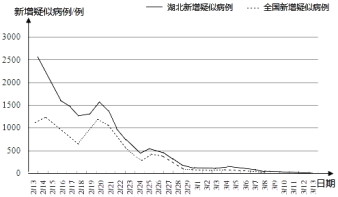
【题目】新冠肺炎疫情暴发后,一场同时间赛跑、与病魔较量的战役随即打响.在疫情防控一线,除了广大医务工作者义无反顾、日夜奋战之外,在另一条战线上,科研人员也在加班加点、紧急攻关.全国科技战线积极响应党中央号召,科技、卫健等12个部门组成科研攻关组,短短一个月的时间内就取得了积极进展.3月13日0﹣24时,31个省(自治区、直辖市)和新疆生产建设兵团新增确诊病例11例(数据不含港澳台),新增疑似病例17例(数据不含港澳台).如图是根据国家卫健委关于新型冠状病毒肺炎通报的数据(数据不含港澳台)绘制的统计图:
根据以上信息,回答下列问题:
(1)下列推断合理的是_______.
①2月15日武汉新增确诊病例约为1500例;
②从2月23日起到3月13日止,武汉每日新增确诊病例都在500例以下;
③从2月23日起到3月13日止,全国每日新增疑似病例逐渐减少.
④3月13日湖北新增疑似病例不超过17例.
(2)结合本题的信息及当前防疫形势,说说你的感受.
查看答案和解析>>
科目:初中数学 来源: 题型:
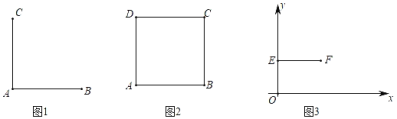
【题目】已知线段AB,如果将线段AB绕点A逆时针旋转90°得到线段AC,则称点C为线段AB关于点A的逆转点.点C为线段AB关于点A的逆转点的示意图如图1:
(1)如图2,在正方形ABCD中,点_____为线段BC关于点B的逆转点;
(2)如图3,在平面直角坐标系xOy中,点P的坐标为(x,0),且x>0,点E是y轴上一点,点F是线段EO关于点E的逆转点,点G是线段EP关于点E的逆转点,过逆转点G,F的直线与x轴交于点H.
①补全图;
②判断过逆转点G,F的直线与x轴的位置关系并证明;
③若点E的坐标为(0,5),连接PF、PG,设△PFG的面积为y,直接写出y与x之间的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆![]() 于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.
于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.

小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的长度这三个量中,确定________的长度是自变量,________的长度和________的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;

(3)结合函数图象,解决问题:当OD=2BC时,线段AP的长度约为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com