
【题目】已知关于x的方程ax2+2x﹣3=0有两个不相等的实数根.
(1)求a的取值范围;
(2)若此方程的一个实数根为1,求a的值及方程的另一个实数根.
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】(2017江苏省常州市)为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如下统计图:

根据统计图所提供的信息,解答下列问题:
(1)本次抽样调查中的样本容量是 ;
(2)补全条形统计图;
(3)该校共有2000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
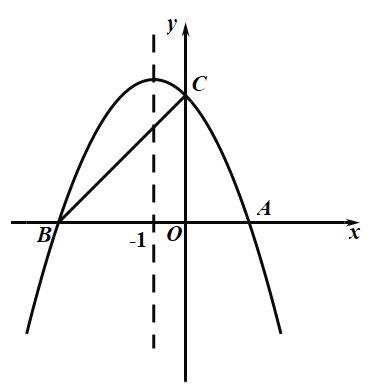
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,它的对称轴是直线
,它的对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 为等腰三角形,请求出符合条件的所有点
为等腰三角形,请求出符合条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)请在图①的![]() 的边
的边![]() 上求作一点
上求作一点![]() ,使
,使![]() 最短;
最短;
(2)如图②,点![]() 为
为![]() 内部一点,且满足
内部一点,且满足![]() .求证:点
.求证:点![]() 到点
到点![]() 、
、![]() 、
、![]() 的距离之和最短,即
的距离之和最短,即![]() 最短;
最短;
问题解决
(3)如图③,某高校有一块边长为400米的正方形草坪![]() ,现准备在草坪内放置一对石凳及垃圾箱在
,现准备在草坪内放置一对石凳及垃圾箱在![]() 点处,使点
点处,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和最小,那么是否存在符合条件的点
三点的距离之和最小,那么是否存在符合条件的点![]() ?若存在,请作出点
?若存在,请作出点![]() 的位置,并求出这个最短距离;若不存在,请说明理由.
的位置,并求出这个最短距离;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
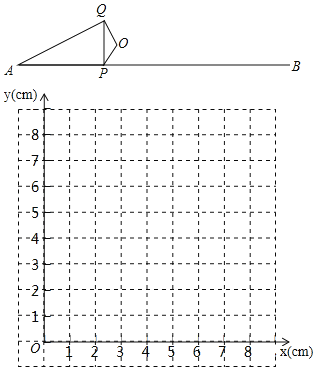
【题目】如图,P是线段AB上的一点,AB=6cm,O是AB外一定点.连接OP,将OP绕点O顺时针旋转120°得OQ,连接PQ,AQ.小明根据学习函数的经验,对线段AP,PQ,AQ的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,PQ,AQ的长度(单位:cm)的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PQ | 4.00 | 2.31 | 0.84 | 1.43 | 3.07 | 4.77 | 6.49 |
AQ | 4.00 | 3.08 | 2.23 | 1.57 | 1.40 | 1.85 | 2.63 |
在AP,PQ,AQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;/span>
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当AQ=PQ时,线段AP的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
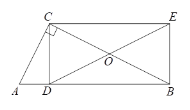
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE∥AB,EB∥CD,连接DE交BC于点O.
(1)求证:DE=BC;
(2)如果AC=5,![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)抛物线的对称轴为_______;
(2)若当![]() 时,
时,![]() 的最小值是
的最小值是![]() ,求当
,求当![]() 时,
时,![]() 的最大值;
的最大值;
(3)已知直线![]() 与抛物线
与抛物线![]() 存在两个交点,设左侧的交点为点
存在两个交点,设左侧的交点为点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+4ax+b(a>0)的顶点A在x轴上,与y轴交于点B.
(1)用含a的代数式表示b;
(2)若∠BAO=45°,求a的值;
(3)横、纵坐标都是整数的点叫做整点.若抛物线在点A,B之间的部分与线段AB所围成的区域(不含边界)内恰好没有整点,结合函数的图象,直接写出a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com