
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线的对称轴;
(3)已知点![]() .若抛物线与线段
.若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的取值范围是
的取值范围是![]()
【解析】
(1)与![]() 轴的交点横坐标为0,然后计算
轴的交点横坐标为0,然后计算![]() 时的函数值即可求出坐标;
时的函数值即可求出坐标;
(2)根据抛物线的对称轴为![]() 求解即可;
求解即可;
(3)由N点和A点的坐标,可知点A在点N的上方,令抛物线上的点![]() ,可得
,可得![]() ,分a>0,a<0两种情形分别求解即可解决问题.
,分a>0,a<0两种情形分别求解即可解决问题.
解:(1)∵抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
令![]() ,得
,得![]() .
.
![]() .
.
(2)由抛物线![]() 可知
可知![]() .
.
∴抛物线的对称轴为直线![]() .
.
(3)对于任意的实数![]() ,都有
,都有![]() .
.
可知点![]() 总在点
总在点![]() 的上方.
的上方.
令抛物线上的点![]() .
.
![]() .
.
①如图1,当![]() 时,
时, ![]() .
.
∴点![]() 在点
在点![]() 的上方.
的上方.
结合函数图象,可知抛物线与线段![]() 没有公共点.
没有公共点.

②当![]() 时
时
(i)如图2,当抛物线经过点![]() 时,
时, ![]() .
.
![]() .
.
结合函数图象,可知抛物线与线段![]() 恰有一个公共点
恰有一个公共点![]() .
.

(ii)当![]() 时,可知抛物线与线段
时,可知抛物线与线段![]() 没有公共点.
没有公共点.
(ⅲ)如图3,当![]() ,时,
,时, ![]() .
.
∴点![]() 在点
在点![]() 的下方.
的下方.
结合函数图象,可知抛物线与线段![]() 恰有一个公共点.
恰有一个公共点.
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
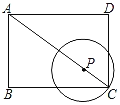
【题目】如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是以点O为圆心,AB为直径的半圆上的动点(不与点A,B重合),AB=6cm,过点C作CD⊥AB于点D,E是CD的中点,连接AE并延长交![]() 于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.
于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.

下面是小腾的探究过程,请补充完整:
(1)对于点C在![]() 上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:
上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
AC/cm | 0.1 | 0.5 | 1.0 | 1.9 | 2.6 | 3.2 | 4.2 | 4.9 |
CD/cm | 0.1 | 0.5 | 1.0 | 1.8 | 2.2 | 2.5 | 2.3 | 1.0 |
FD/cm | 0.2 | 1.0 | 1.8 | 2.8 | 3.0 | 2.7 | 1.8 | 0.5 |
在AC,CD,FD的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;

(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解答问题:当CD>DF时,AC的长度的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地扶贫人员甲从办公室出发,骑车匀速前往所![]() 村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往
村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往![]() 村.甲、乙两人相距的路程
村.甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列三个说法:
(分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列三个说法:

①甲出发10分钟后与乙相遇;
②甲的速度是400米/分;
③乙返回办公室用时4分钟.
其中所有正确说法的序号是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度.其中斜坡轨道BC的坡度(或坡比)为i=1:2,BC=12![]() 米,CD=8米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
米,CD=8米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
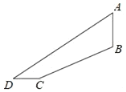
A.5.6B.6.9C.11.4D.13.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形网格中,点A,B,M,N都在格点上.从点M,N中任取一点,与点A,B顺次连接组成一个三角形,则下列事件是必然事件的是( )
的正方形网格中,点A,B,M,N都在格点上.从点M,N中任取一点,与点A,B顺次连接组成一个三角形,则下列事件是必然事件的是( )
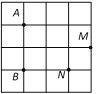
A.所得三角形是锐角三角形B.所得三角形是直角三角形
C.所得三角形是钝角三角形D.所得三角形是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com